Kartenprojektionen vergleichen

[info]    Ansichtsoptionen: Süden oben    Flache Ozeane    Setzen

Wagners Netzentwürfe (Teil 3): Das Umbeziffern

Teil 3 dieser Artikel-Serie sollte sich eigentlich einigen Wagner-Varianten von Frank Canters und Dr. Rolf Böhm widmen. Zum besseren Verständnis der Varianten erschien es mir aber angebracht, zunächst die Methode zu erklären, die Wagner beim Entwurf seiner eigenen neuen Projektionen verwendet hat: Das Umbeziffern.

Karlheinz Wagner hat das Umbeziffern 1949 ^[1] ausführlich vorstellt, eine gute Zusammenfassung stammt von Frank Canters ^[2]:

The transformation method is based on a very simple idea, but provides a powerful mechanism for the development of new map projections. First a well-chosen part of the graticule of an existing projection, bounded by an upper an a lower parallel, and a left and right meridian, is selected. The entire area to be represented is mapped onto this part of the graticule by redefinition of the longitude and latitude values of each meridian and parallel (Umbeziffern). Then the graticule is enlarged to the original scale of the parent projection. Restoration of the original scale may be followed by an affine transformation in the x- and y-direction. This permits control of the ratio of the axes of the projection.

Eine freie Übersetzung meinerseits:

Die Transformationsmethode basiert auf einer ganz einfachen Idee, bietet aber einen mächtigen Mechanismus zur Entwicklung neuer Kartenprojektionen. Zunächst nimmt man einen gut gewählten Ausschnitt aus einer vorhandenen Projektion, der durch einen oberen und einen unteren Breitenkreis sowie einen linken und rechten Meridian definiert wird. Die gesamte Fläche, die dargestellt werden soll, wird nun auf diesen Teil des Gradnetzes projiziert, indem man die Längen- und Breitengrade jedes Meridians und Breitenkreises neu definiert (umbeziffert). Das resultierende Gradnetz wird anschließend vergrößert, um es wieder auf den Maßstab der Ausgangsprojektion zu bringen. Anschließend kann man eine affine Transformation der x- und y-Koordination vornehmen. Dies erlaubt es, das Längenverhältnis der Achsen der neuen Projektion zu kontrollieren.

Wir schauen uns diesen Vorgang anhand einiger Illustrationen an – und nehmen als Beispiel die Konstruktion des Wagner VII.
 

Umbeziffern, Schritt für Schritt

Als Ausgangsprojektion entschied sich Wagner für den querachsigen flächentreuen Azimutalentwurf. Als Ausschnitt, der transformiert werden sollte, wählte er den Bereich zwischen 65° Nord/Süd und 60° Ost/West.

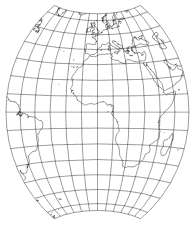
Die dazustellende Fläche – in diesem Fall: die gesamte Erde – wird auf diesen Ausschnitt projiziert, der umbezifferte Ausschnitt wird wieder auf den Maßstab des Ausgangsentwurfs gebracht:

Der umbezifferte Ausschnitt wird in Richtung der Koordinatenachsen verdehnt. Dabei wird die Eigenschaft der Flächentreue des Ausgangsentwurfs beibehalten. Als Resultat erhalten wird den Wagner VII:

Der neue Entwurf wird also bisher durch verschiedene Parameter determiniert:

1. Den Ausgangsentwurf;
2. den begrenzenden Breitenkreis;
3. den begrenzenden Meridian;
4. und den Verdehnungsfaktor, welcher das Längenverhältnis von Zentralmeridian zum Äquator regelt.

Innerhalb dieses Artikel konzentrieren wir uns auf Wagner VII und VIII, die auf dem querachsigen flächentreuen Azimutalentwurf basieren. Der erste Parameter fällt im folgenden also weg, da er feststeht. Bleiben für den Moment drei übrig.

Bevor es weitergeht, möchte ich noch festhalten, dass der gewählte begrenzende Breitenkreis faktisch die Länge der Pol-Linie unserer neuen Projektion bestimmt – während der begrenzenden Meridians die Krümmung der Breitenkreise beeinflusst. Um das zu verdeutlichen, schauen wir uns den gewählten Ausschnitt an, wenn er statt 65 bei 80° Nord/Süd begrenzt ist; und wenn er bei 90° Ost/West begrenzt wurde:

Der Ausgangsentwurf, beschnitten auf 80° N/S und 60° O/W (links)
und beschnitten auf 65° N/S, 90° O/W (rechts).
 

Es ist also offensichtlich, dass höhere Gradzahlen des begrenzenden Breitenkreises zu einer kürzeren Pollinie des neuen Entwurfs führen werden, und höhere Gradzahlen des begrenzenden Meridians zur einer stärkeren Krümmung der Breitenkreise.

Machen wir weiter:
Der Wagner VII ist, wie gesagt, wie die Ausgangsprojektion flächentreu. Also hat Wagner zwei weitere Parameter hinzugefügt, mit denen man eine kontrollierte Flächenverzerrung in den neuen Entwurf einbringen kann:

Man kann nun vorschreiben, dass beim Parallelkreis φ₁ die Flächenverzerrung nicht größer als S₁ sein soll (…)

Für die Projektion, die wir heute als Wagner VIII kennen, hat Wagner φ₁ = 60 und S₁ = 1,2 festgelegt; also eine Flächenvergrößerung von 20% auf 60° Nord/Süd. Die Werte wurden gewählt, da man zwischen ± 60° »ungefähr den bewohnten Teil der Erde erfasst« und »eine Flächenvergrößerung von 20% für das angegebene Gebiet noch tragbar ist«.

Die endgültige Liste umfasst also nun fünf Konfigurationsparameter – und diesmal fügen wir noch die in der kartografischen Literatur üblichen Notationen hinzu:

1. Der begrenzende Parallelkreis: ψ₁
2. Der begrenzende Meridian: λ₁
3. Der Referenz-Breitengrad für die Flächenverzerrung: φ₁
4. Das Ausmaß der Flächenvergrößerung auf φ₁: S₁
5. Das Achsenverhältnis: p

 

Und nun beginnst Du sicher schon zu ahnen, wie die eingangs erwähnten Herren Canters und Böhm bei ihren Wagner-Varianten vorgegangen sind: Richtig, sie haben an genau diesen fünf Parametern herumgedreht. Ihre Ergebnisse werde ich im ausstehenden vierten fünften Teil dieser Artikelserie behandeln.
Aber vorher muss ich noch ein paar andere Dinge loswerden.

 

Notation

In der kartografischen Literatur findet man oft den Begriff der Wagner-Konstanten (o.ä.) – denn die Formeln, die Wagner für seine Entwürfe benutzt hat, enthalten einige numerischen Werte, wie hier für den Wagner VIII:

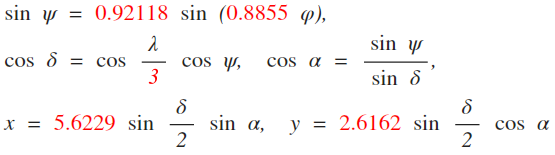
Die genannten Konstanten habe ich in roter Schrift hervorgehoben.
Aber wie kam Wagner eigentlich zu diesen numerischen Werten?
Nun, er nahm sich seine fünf Eingangs-Parameter, berechnete damit einige Formeln, und bekam am Ende ein paar numerische Werte heraus, die er zum Vorteil des Lesers in die endgültige Formel einsetze. Aber natürlich kann man mit diesen numerischen Werten nur den Wagner VIII berechnen. Stattdessen könnte man die Formel auch in einer allgemeinen Form schreiben:

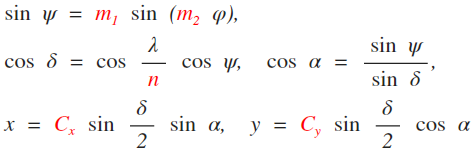
In diese allgemeine Form muss man nun noch die richtigen Werte für m₁, m₂, C_x, C_y und n eintragen – und schon hat man eine Wagner-Variante, wie z.B. jene von Canters und Böhm. Und wie kommt man an diese Werte? – Man berechnet sie aus den fünf o.g. Konfigurationsparametern, wie z.B. Dr. Böhm in ^[3] gezeigt hat (Formeln 7 bis 12).

Und es gibt noch einen anderen Weg, an diese Werte zu kommen.
Aber warte noch einen Augenblick, ich komme gleich darauf zurück.

Ich möchte vorher nämlich noch erwähnen, dass Dr. Böhm eine sehr praktische Notation vorgeschlagen hat, um Wagner-Varianten zu identifizieren: Eine einfache Liste der 5 Konfigurationsparameter, getrennt durch einen Bindestrich. Die ersten drei Parameter übernehmen dabei ihre üblichen Werte in Grad, für Nr. 4 und 5 hat sich Böhm für prozentuale Werte entschieden. Eine Flächenvergrößerung von 1,2 wird folglich als 20 geschrieben; soll der Äquator doppelt so lang sein wie der Zentralmeridian, wird dies als 200 notiert.
In diesem Schema wird der Wagner VII als 65-60-60-0-200 geschrieben, der Wagner VIII als 65-60-60-20-200.

Ich halte dies für eine sehr gute Idee, denn erstens kann man sich diese Werte leichter merken als etwa die Konstanten (0,92118 usw.) – vor allem aber haben sie einen direkten Bezug zum Ausgangsentwurf; und wenn man die oben gezeigten Schritt-für-Schritt-Grafiken im Kopf behält, kann man sich sogar (wenigstens annähernd) vorstellen, wie etwa die Konfiguration 65-84-60-25-200 aussehen könnte, bevor man sie tatsächlich gesehen hat.

Ein kleiner Nachteil dieses Verfahrens ist es, dass unterschiedliche Notationen identische Projektionen beschreiben, d.h. es ist nicht ein-eindeutig. Zum Beispiel hat der Wagner VIII, wie gesagt, eine Flächenvergrößerung von 1,2 bei 60°. Das entspricht 1,89 bei 80°. Den Wagner VIII kann man also nicht nur als 65-60-60-20-200 schreiben, sondern auch als 65-60-80-89-200. Diese Mehrdeutigkeit könnte man umgehen, indem man sich darauf einigt, entweder nur die Flächenvergrößerung bei 60° zu notieren – der Wagner VIII würde dann also durch 65-60-20-200 spezifiziert – oder andersherum, stets jenen Breitengrad zu nennen, auf dem die Flächenvergrößerung genau 20% beträgt (65-60-60-200).

Dr. Böhm hat in seinem Artikel darauf auch hingewiesen, sich aber dennoch entschlossen, alle fünf Parameter zu notieren, um die Verständlichkeit zu wahren. Ich kann dieser Entscheidung nur zustimmen, schlage aber dringend vor, dass jeder, der diese Notationen übernehmen will, als dritten Parameter stets 60 notieren möge.

Eine kleine Anmerkung:
Ich selbst hätte es bevorzugt, die Parameter Nr. 4 und 5 als Faktor zu schreiben und nicht in Prozent. Der Wagner VIII würde somit als 65-60-60-1.2-2 notiert und nicht als 65-60-60-20-200. Der Grund dafür ist ganz einfach: Die 20% fühlen sich für mich wie eine Verkleinerung an. Natürlich verstehe ich, dass der originale Wert um 20% erhöht wird und nicht auf 20% verkleinert. Aber ich bin der Meinung, dass der Faktor hier leichter zu erfassen gewesen wäre.
Dennoch übernehme ich die Notation, so wie sie Dr. Böhm vorgeschlagen hat. Schließlich ist er der Profi in Sachen Kartennetzentwürfen und nicht ich. Sie wurde in einem kartographischen Fachmagazin vorgestellt, und es wäre mir anmaßend vorgekommen, nun zu rufen: »Ha! Ich weiß es besser!«

 

… und die anderen Wagner-Entwürfe?

Nun habe ich das Umbeziffern anhand des Wagner VII gezeigt und wie man daraus den Wagner VIII ableitet.
Da Wagner aber alle neun nach ihm benannten Entwürfe durch Umbeziffern generiert hat, kann man sie alle auf die o.g. Weise modifizieren. Allerdings stehen dabei weniger Parameter zur Verfügung:

• Bei allen neun Projektionen kann man die Länge der Pollinie und das Achsenverhältnis ändern – letzteres entspricht bei den Pseudozylindern faktisch einer Änderung der Schnittparallele.
• Wagner I bis Wagner VI sind von pseudozylindrischen Ausgangsentwürfen abgeleitet, folglich haben sie stets gerade Parallelkreise – es gibt keinen Parameter, der die Krümmung beeinflusst.
• Außerdem sind Wagner III und Wagner VI abstandsgleich, d.h. sie haben gleichabständige Parallelkreise. Daraus folgt, dass bei ihnen zusätzlich der Parameter, welcher die Flächenvergrößerung festlegt, wegfällt.
• Auch der Wagner IX hat gleichabständige Parallelkreise (entlang des Zentralmeridians), also fällt die variable Flächenvergrößerung ebenfalls weg. Allerdings kann man hier wiederum die Krümmung der Parallelkreise modifizieren – das macht ihn in meinen Augen zum zweitinteressantesten Wagner-Entwurf für eigene Spielereien.

Infolgedessen schlage ich hiermit eine kleine Erweiterung der Böhm-Notation vor:
Um klarzustellen, welchen Wagner-Entwurf man modifiziert, wird dessen römische Ordnungszahl in Kleinschreibung vorangestellt, gefolgt vom @-Zeichen. Eine Variation des Wagner VII würden dann z.B. geschrieben als
Wagner vii@65-84-60-25-200,
ein Derivat des Wagner IX hingegen wäre beispielsweise
Wagner ix@67-87-200-82.

Ich ziehe die Kleinschreibung der römischen Ziffer vor, um anzudeuten, dass es sich nicht um die originale Ausführung von Wagner handelt.
Und beachte, dass Wagner II, V und VIII ihrerseits Varianten von Wagner I, IV und VII (in dieser Reihenfolge) darstellen, also solltest Du nie die Präfixe ii@, v@ und viii@ verwenden, sondern stets die jew. vorhergehende Zahl.

Zugegeben, es ist ein wenig … seltsam, die Erweiterung einer Notation vorzuschlagen, die – nach meiner Kenntnis – außer Dr. Böhm und mir selbst ohnehin noch nie irgendjemand benutzt hat. Aber immerhin weißt Du jetzt, was ich meine, wenn ich in Zukunft diese erweiterte Schreibweise benutze…

 

Generiere Deine eigenen Wagner-Variationen – Der WVG

Hoffentlich bist Du nun ein wenig neugierig geworden, wie Wagner-Variationen aussehen könnten. Denn habe ich etwas für Dich: Den Wagner-Variationen-Generator (WVG). Dort kannst Du die Konfigurationsparameter (fast) nach Belieben ändern und nach Klick auf den »Generiere Projektion«-Button wird eine Grafik der resultierenden Projektion erzeugt.
Er steht in zwei Varianten zur Verfügung: Der WVG-7 variiert den Wagner VII (und somit, s.o, den Wagner VIII);
der WVG-9 basiert auf dem Wagner IX.

Außer eigenen Werten kann man per Klick eine Reihe von vordefinierten Projektionen auswählen, die sich aus Wagners Formel erzeugen lassen. Die kannst Du z.B. als Ausgangspunkt für Deinen eigenen Experimente verwenden.

Darüber hinaus stehen noch graphische Optionen zur Verfügung, welche nicht die Projektion an sich, aber ihre Darstellung beeinflussen: Die Darstellung der Kontinente (als graue Silhouette, in Umrissen, mit farbiger Anzeige der Staaten, oder ganz ohne Kontinente, so dass Du nur das Gradnetz siehst); die Schrittweite des Gradnetzes; die Skalierung der erzeugten Grafik. Zum Vergleich kannst Du auch eine Hintergrund-Grafik mit einer anderen Projektion anzeigen lassen – zur Verfügung stehen dabei alle zylindrischen, pseudozylindrischen und lentikulären Entwürfe, die hier auf der Website integriert sind.
Die erzeugte Projektion kannst Du dann als SVG-Datei herunterladen.

Aber was rede ich hier überhaupt rum?
Geh rüber zum Wagner-Variationen-Generator 7 oder Wagner-Variationen-Generator 9 und probier ihn aus…
 

Falls Du Dich wunderst, warum Du beim WVG-7 nur vier von fünf Parametern ändern kannst und nicht alle:
Da ich selbst vorgeschlagen habe, den Referenz-Breitengrad für die Flächenverzerrung φ₁ stets mit 60 zu notieren, erschien es mir ratsam, diesen Wert beizubehalten. Darüber hinaus hilft diese Festlegung auch, Fehler zu vermeiden: Bei φ₁ = 60 beträgt der maximale Wert für die Flächenvergrößerung (S₁) 99,999%. Darüber hinaus kann keine Grafik mehr erzeugt werden (eine Arkuskosinus-Funktion wird ansonsten mit einem ungültigen Wert gefüttert).
Bei φ₁ = 80 liegt der Maximalwert der Flächenvergrößerung hingegen bei 475,877. Genauer gesagt ist bei jedem Wert von φ₁ ein anderer Maximalwert möglich – wobei aber immer das gleiche Resultat erzeugt wird. Um die unbefriedigende Situation zu vermeiden, dass man Werte eingibt, die keine Projektion erzeugen können, habe ich also die 60 für den Breitengrad festgenagelt und die Maximalwert für die Verzerrung auf 99,999 gesetzt.

 

Und noch ein paar Worte

Wagners Umbeziffern ist ein mächtiges Werkzeug, um Projektionen nach eigenen Wünschen und Bedürfnissen zu gestalten. Aber es hat auch Grenzen: Man wird nie der grundsätzlichen Charakteristik des Ausgangsentwurfs entkommen. Beispielsweise lässt sich der Abstand der Meridiane nicht verändern oder variieren; auch Kurvenformen wie beim Hufnagel-System (siehe den entsprechenden Artikel oder das interaktive Hufnagel-Tool auf mapthematics.com) sind unmöglich.

Und wenn Du nicht nur mit Wagner-Variationen herumspielen, sondern echte Karten erzeugen willst:
Ab Version 3.2 der Kartenprojektions-Software Geocart ist der generalized Wagner verfügbar, der eine Modifikation des Wagner VII nach dem hier gezeigten Schema darstellt. Er wird allerdings nicht die Böhm-Notation verwenden. Aber keine Sorge: Im WVG-7 wird die Böhm-Notation in die Werte, die Du in Geocart eingeben musst, umgerechnet.

 
Und nebenbei…
Habe ich Dich schon aufgefordert, den WVG-7 und den WVG-9 auszuprobieren? ;-)

 

Quellenangaben

1. ↑ Wagner, Karlheinz:
   Kartographische Netzentwürfe.
   Leipzig 1949.
2. ↑ Canters, Frank:
   Small-scale Map Projection Design.
   London & New York 2002.
3. ↑ Dr. Rolf Böhm:
   Variationen von Weltkartennetzen der Wagner-Hammer-Aitoff-Entwurfsfamilie
   Erstveröffentlichung in: Kartographische Nachrichten Nr. 1/2006. Kirschbaum: Bonn-Bad Godesberg.
   Zitiert nach www.boehmwanderkarten.de/archiv/pdf/boehm_kn_2_2006_2015_complete.pdf

 

Zurück zu Ausgewählte Entwürfe  •  Wagners Netzentwürfe (Teil 2)  •  Teil 4  •  Nach oben