Meine Projektions-Kollektion:
Kartenprojektionen vergleichen
Cahills konformer Schmetterling vs. Waterman Butterfly (alternatives Arrangement)
| Cahills konformer Schmetterling | Waterman Butterfly (alternatives Arrangement) | |
|---|---|---|
| Urheber | Bernard J. S. Cahill, Oscar S. Adams (ca. 1929) | Steve Waterman (1996) |
| Gruppe | Polyedrische | Polyedrische |
| Eigenschaft | Winkeltreu | Vermittelnd |
| Andere Namen | — | — |
| Anm.Anmerkungen | Cahill entwickelte 1909 seine erste (vermittelnde) Karte in Schmetterlingsform. Auf Cahills Anregung entwickelte Oscar S. Adams Mitte der 1920er Jahre die mathematischen Formeln für die hier gezeigte winkeltreue Variante, welche Cahill 1929 veröffentlichte. In Cahills originalem Arrangement wurde Afrika in den oberen linken »Flügel« gelegt, zur besseren Vergleichbarkeit wurde die hier gezeigte Karte auf 20° West zentriert. Siehe auch Vier winkeltreue polyedrische Projektionen und mehr. |
Inspiriert von der »Butterfly«-Karte von Bernard J. S. Cahill (1903). In der üblichen Darstellung werden die vier Spitzen, welche Antarktika enthalten, abschnitten und unter dem »Schmetterling« inselförmig wieder zusammgesetzt. Mehr dazu im Blogpost. |
| Empfohlene Vergleiche | Cahill konform, M-förmig Waterman Butterfly |
Cahills konformer Schmetterling Cahill-Keyes |
|
Diese Paarung gehört zur Liste der empfohlenen Vergleiche – aber warum? Zwei Schmetterlings-Projektionen – einmal winkeltreu (Cahill), einmal vermittelnd (Waterman). |
||
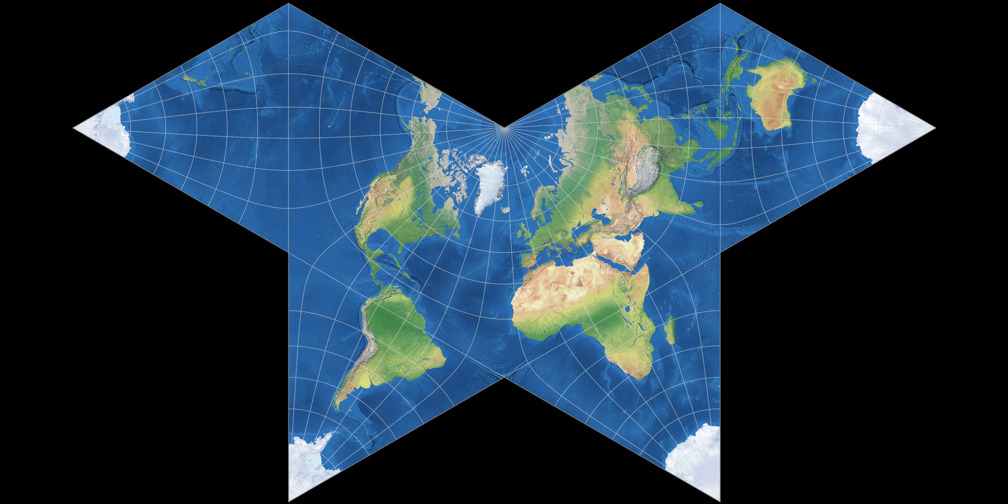
1. Vergleich: Physische Karte – passend skaliert
Cahills konformer Schmetterling c Tobias Jung
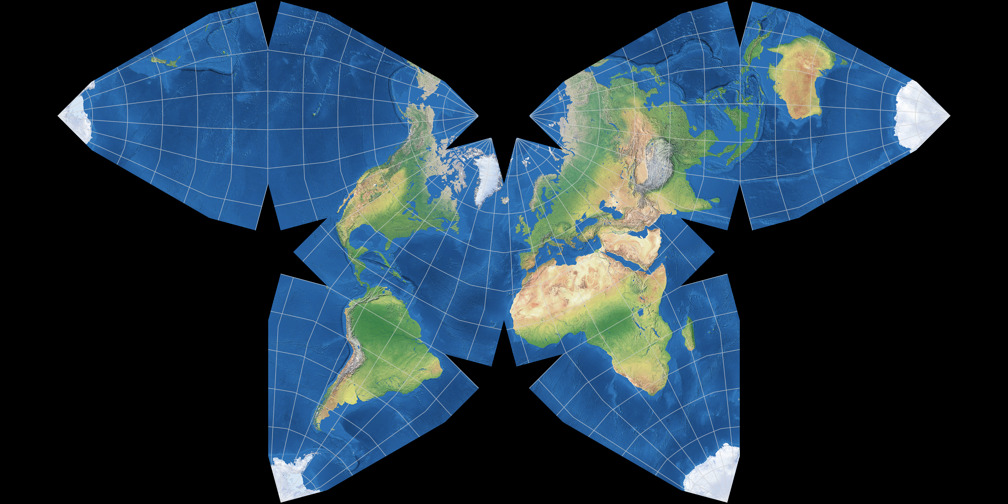
Waterman Butterfly (alternatives Arrangement) c Tobias Jung
2. Vergleich: Politische Karte – passend skaliert
Cahills konformer Schmetterling
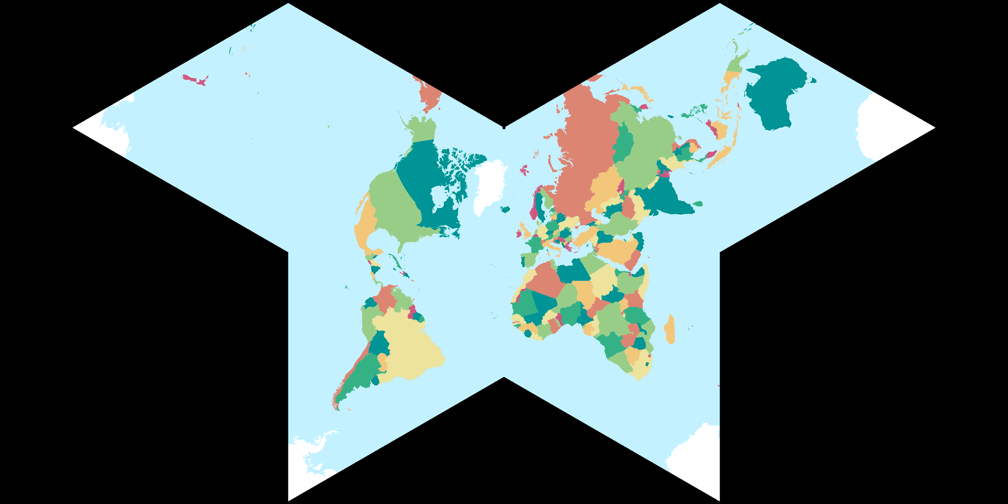
Waterman Butterfly (alternatives Arrangement)

Cahills konformer Schmetterling c Tobias Jung
Waterman Butterfly (alternatives Arrangement) c Tobias Jung
3. Vergleich: Umrisskarte – passend skaliert
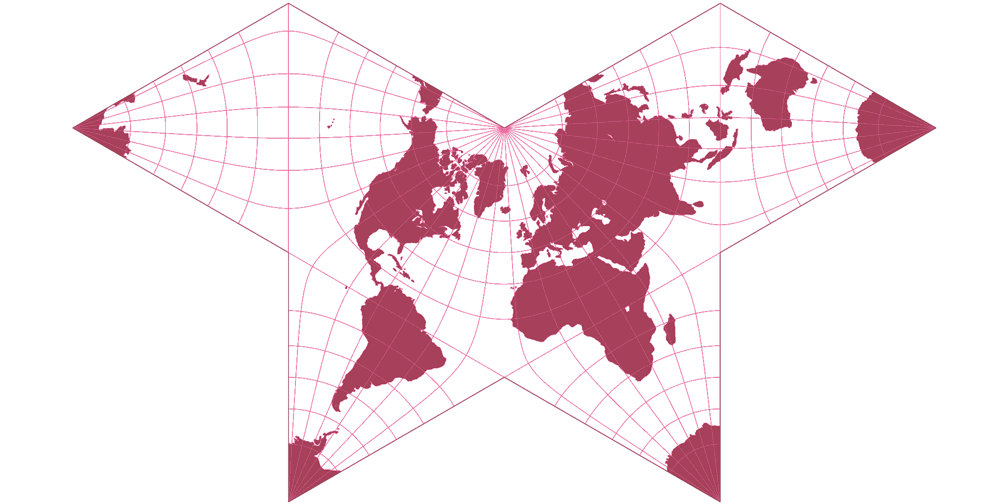
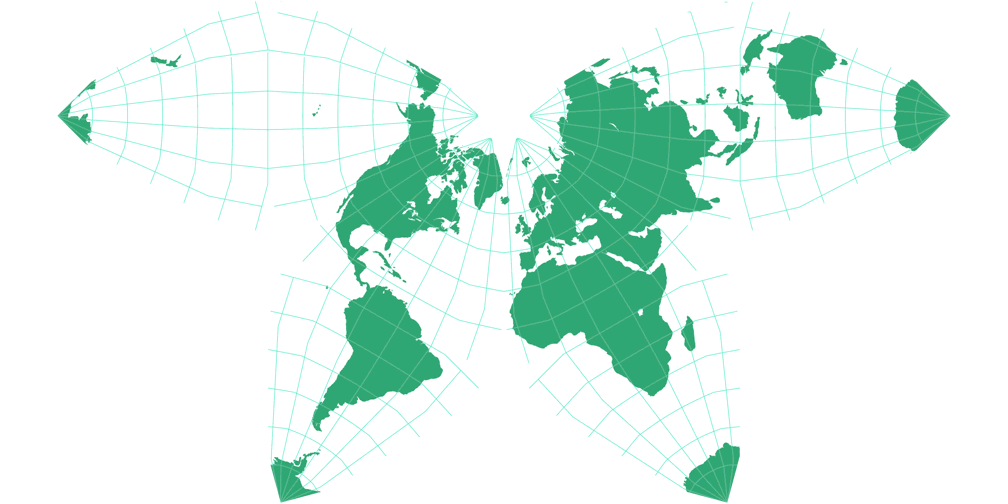
Cahills konformer Schmetterling Umrisskarte c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Umrisskarte c Tobias Jung
4. Vergleich: Tissotsche Indikatrix, 30° – passend skaliert
Cahills konformer Schmetterling

Waterman Butterfly (alternatives Arrangement)
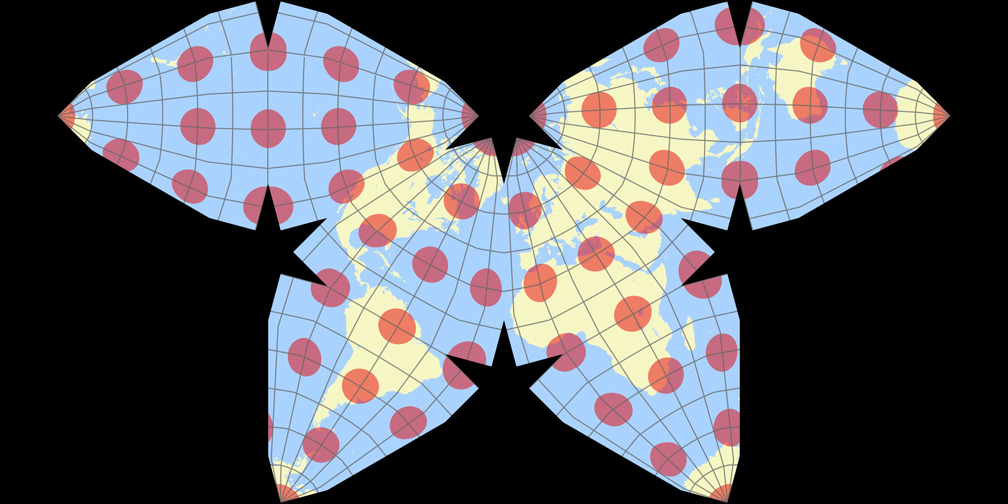
Cahills konformer Schmetterling Tissotsche Indikatrix c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Tissotsche Indikatrix c Tobias Jung
5. Vergleich: Physische Karte – auf gleiche Breite skaliert
Cahills konformer Schmetterling
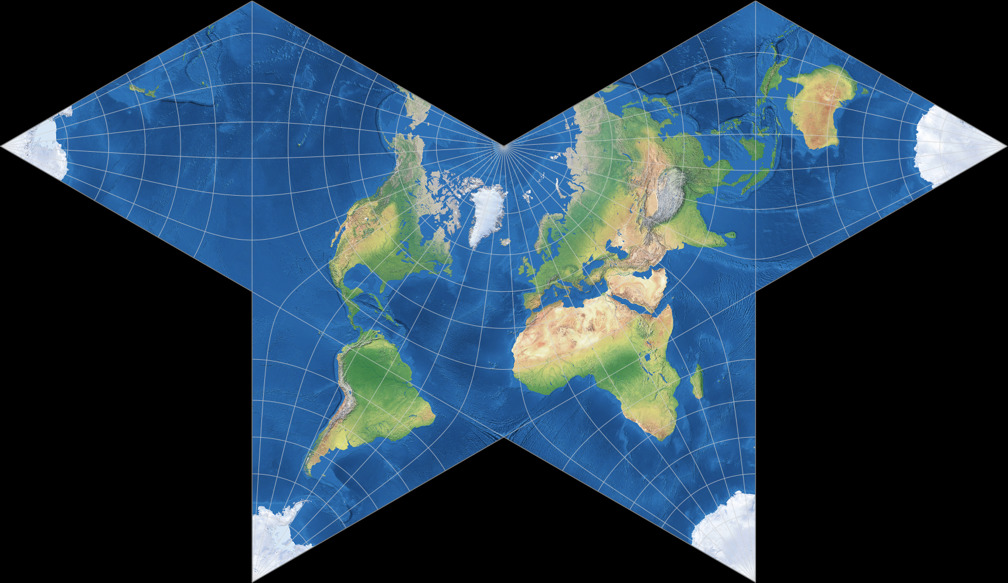
Waterman Butterfly (alternatives Arrangement)
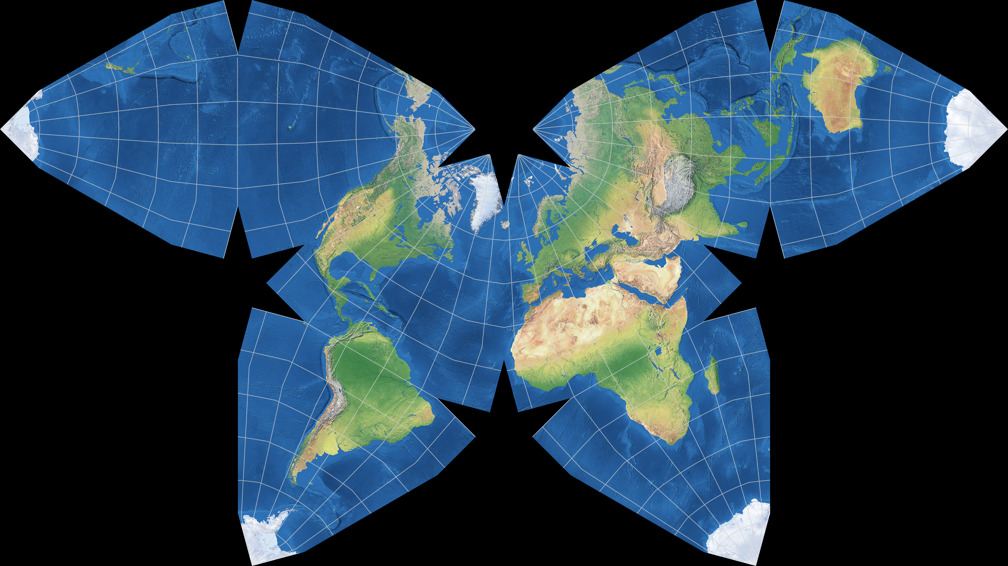
Cahills konformer Schmetterling c Tobias Jung
Waterman Butterfly (alternatives Arrangement) c Tobias Jung
6. Vergleich: Politische Karte – auf gleiche Breite skaliert
Cahills konformer Schmetterling
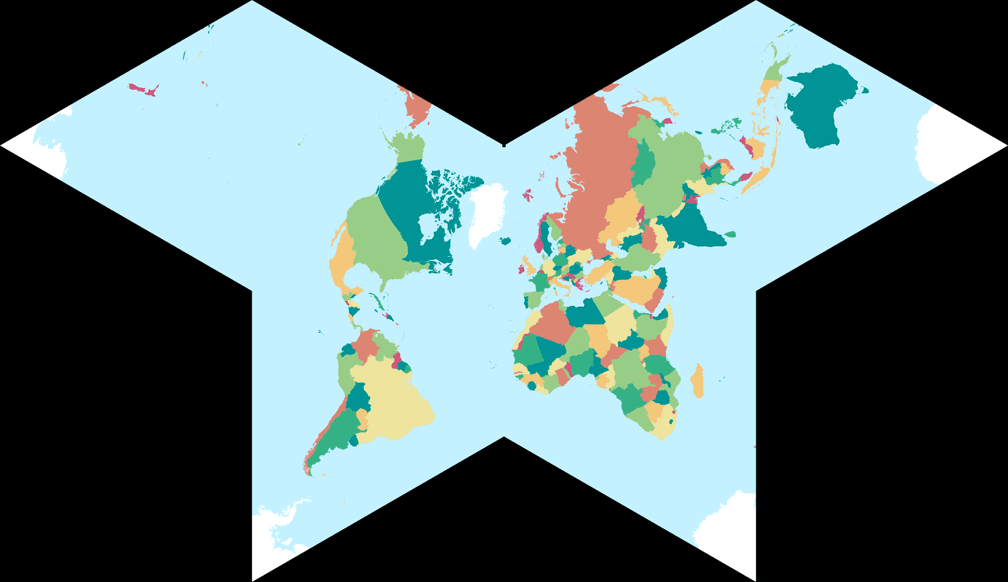
Waterman Butterfly (alternatives Arrangement)
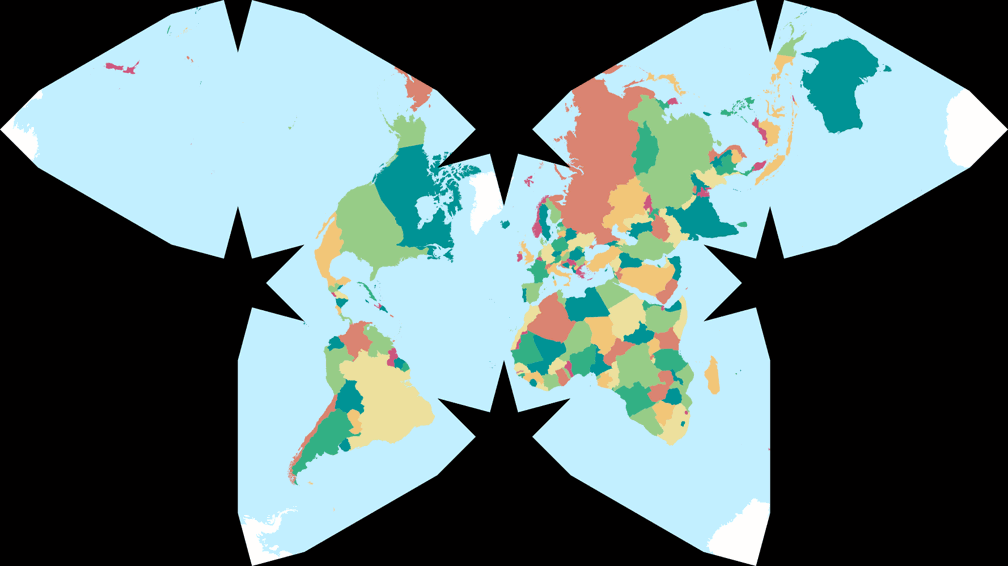
Cahills konformer Schmetterling c Tobias Jung
Waterman Butterfly (alternatives Arrangement) c Tobias Jung
7. Vergleich: Umrisskarte – auf gleiche Breite skaliert
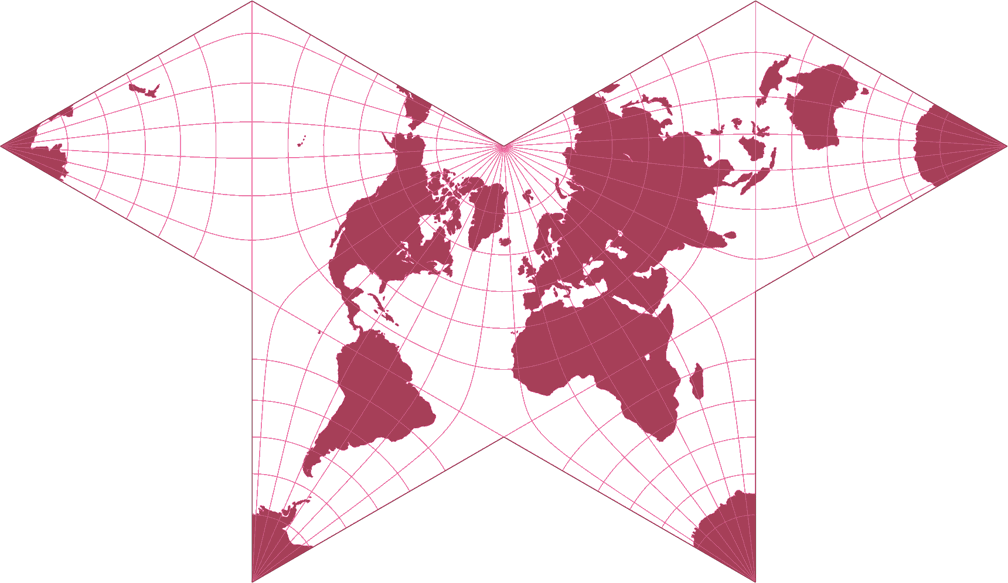
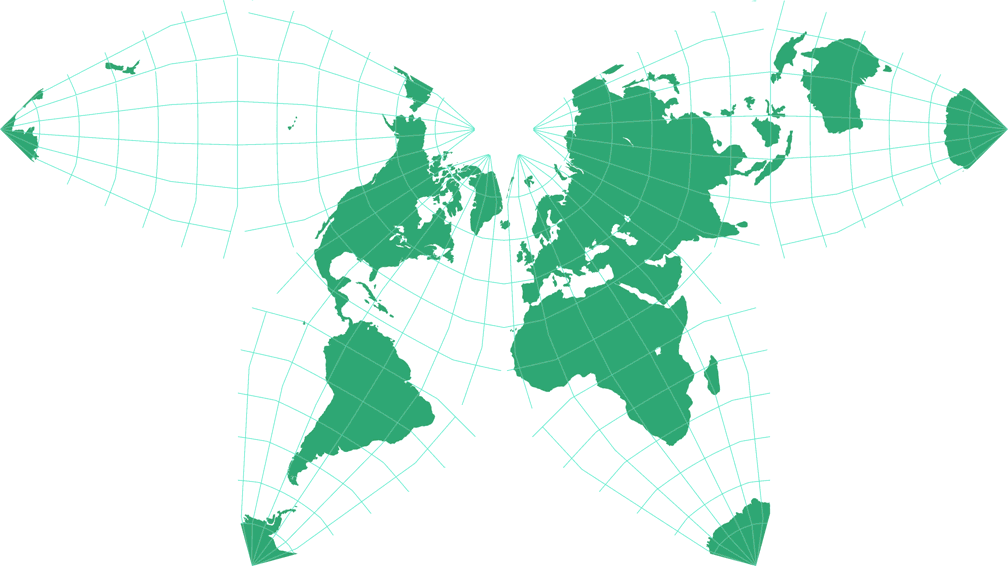
Cahills konformer Schmetterling Umrisskarte c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Umrisskarte c Tobias Jung
8. Vergleich: Tissotsche Indikatrix, 30° – auf gleiche Breite skaliert
Cahills konformer Schmetterling
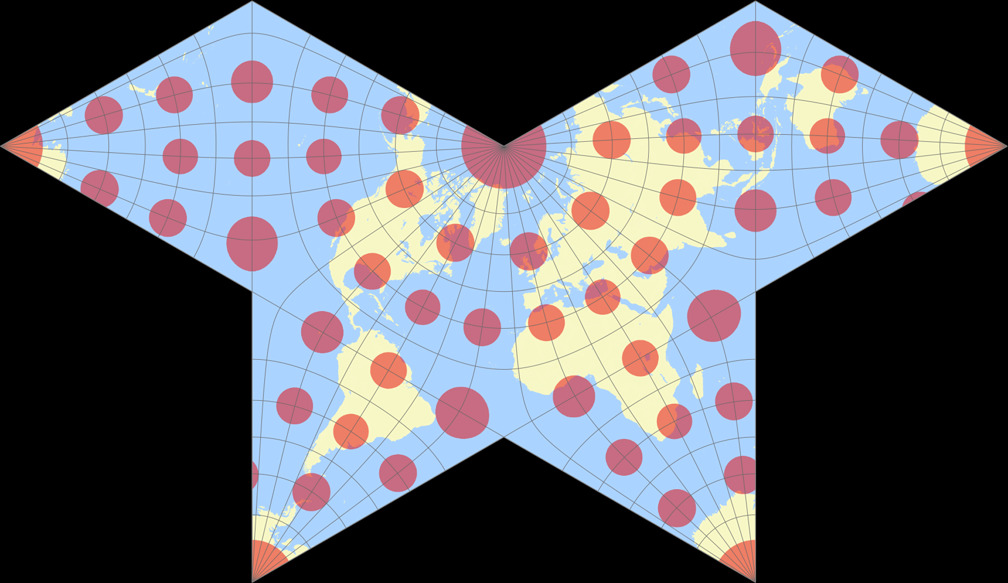
Waterman Butterfly (alternatives Arrangement)
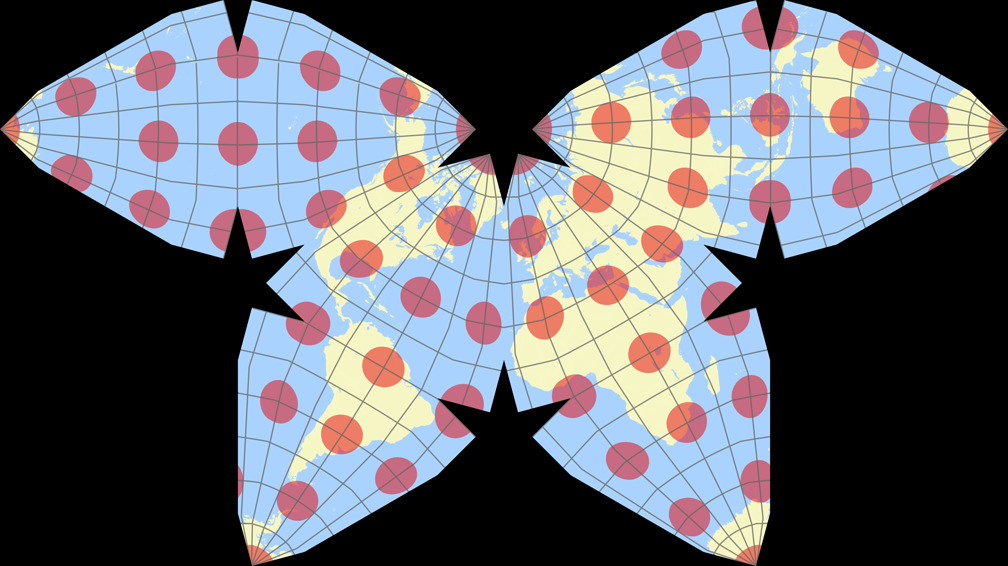
Cahills konformer Schmetterling Tissotsche Indikatrix c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Tissotsche Indikatrix c Tobias Jung
9. Vergleich: Tissotsche Indikatrix, 15° – passend skaliert
Cahills konformer Schmetterling

Waterman Butterfly (alternatives Arrangement)

Cahills konformer Schmetterling Tissotsche Indikatrix c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Tissotsche Indikatrix c Tobias Jung
10. Vergleich: Tissotsche Indikatrix, 15° – auf gleiche Breite skaliert
Cahills konformer Schmetterling

Waterman Butterfly (alternatives Arrangement)

Cahills konformer Schmetterling Tissotsche Indikatrix c Tobias Jung
Waterman Butterfly (alternatives Arrangement) Tissotsche Indikatrix c Tobias Jung