Meine Projektions-Kollektion:
Kartenprojektionen vergleichen
Ginzburg V vs. Rektangular, quadratisch
| Ginzburg V | Rektangular, quadratisch | |
|---|---|---|
| Urheber | G. A. Ginzburg (1950) | Marinus of Tyre (ca. 100 n.Chr.) |
| Gruppe | Lentikulär | Zylinder |
| Eigenschaft | Vermittelnd | Längentreu |
| Andere Namen |
|
|
| Anm.Anmerkungen | — | Abstandstreue Zylinderprojektion mit dem Äquator als Schnittparallele. Der Urheber wird im Deutschen Marinos von Tyros genannt. Ich wollte nur kein eigenes, sprachspezifisches Datenbank-Feld für den Urheber einrichten wegen einer einzigen Projektion, bei der sich der Name in Deutsch und Englisch unterscheidet. ;-) |
| Empfohlene Vergleiche | Canters W14 | Gall Isographisch |
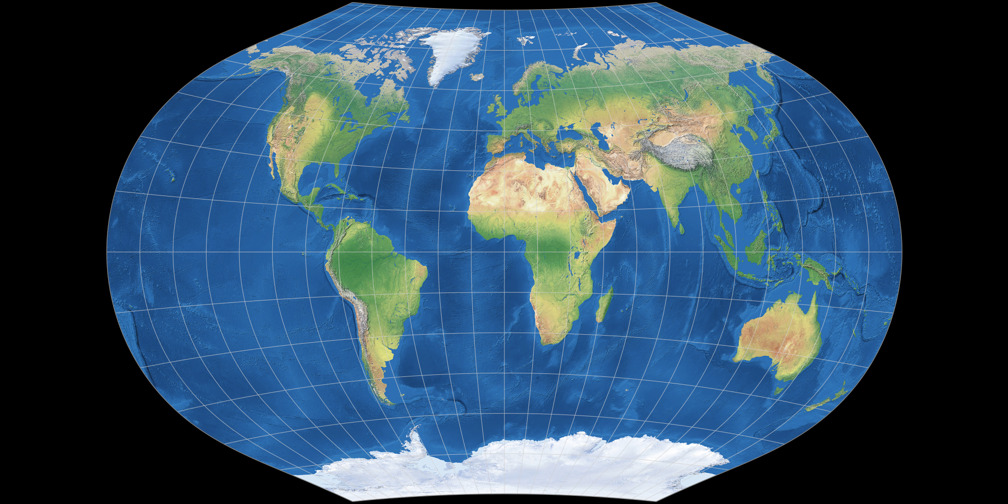
1. Vergleich: Physische Karte – passend skaliert
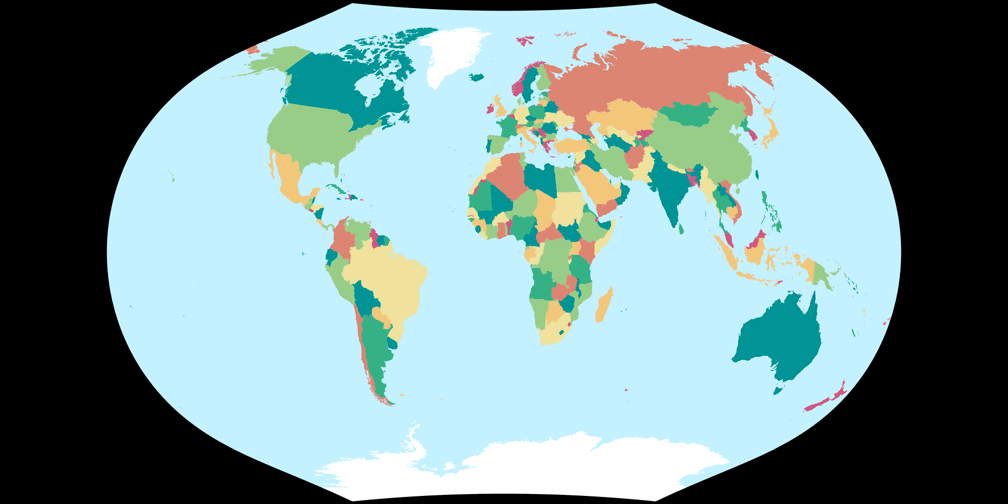
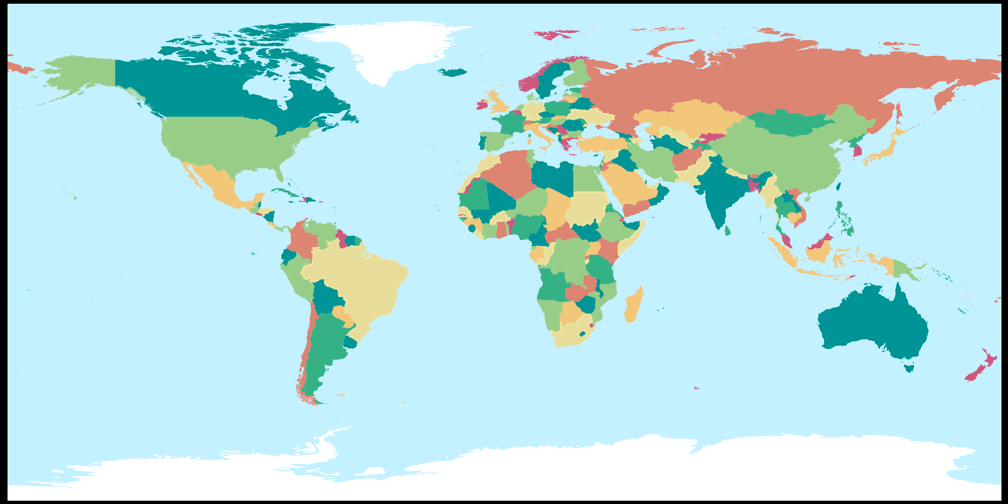
2. Vergleich: Politische Karte – passend skaliert
Ginzburg V
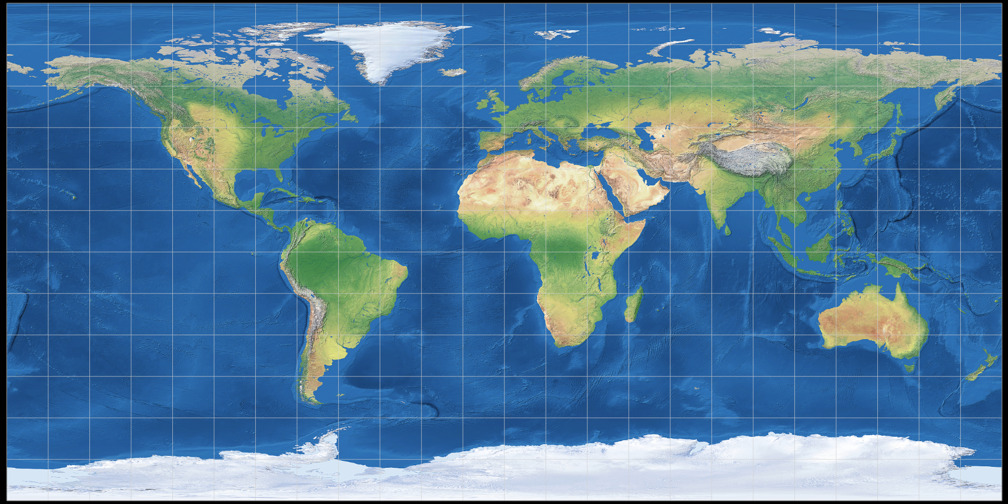
Rektangular, quadratisch
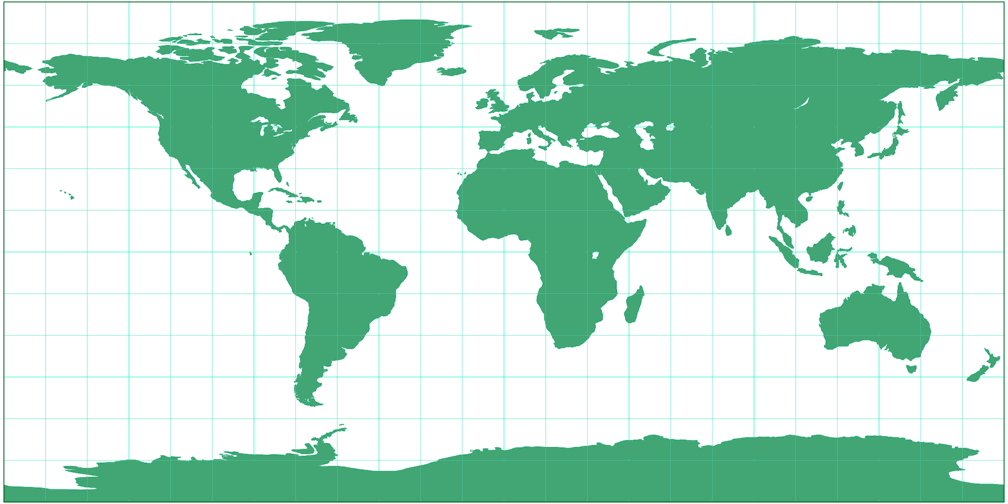
3. Vergleich: Umrisskarte – passend skaliert

4. Vergleich: Tissotsche Indikatrix, 30° – passend skaliert
Ginzburg V
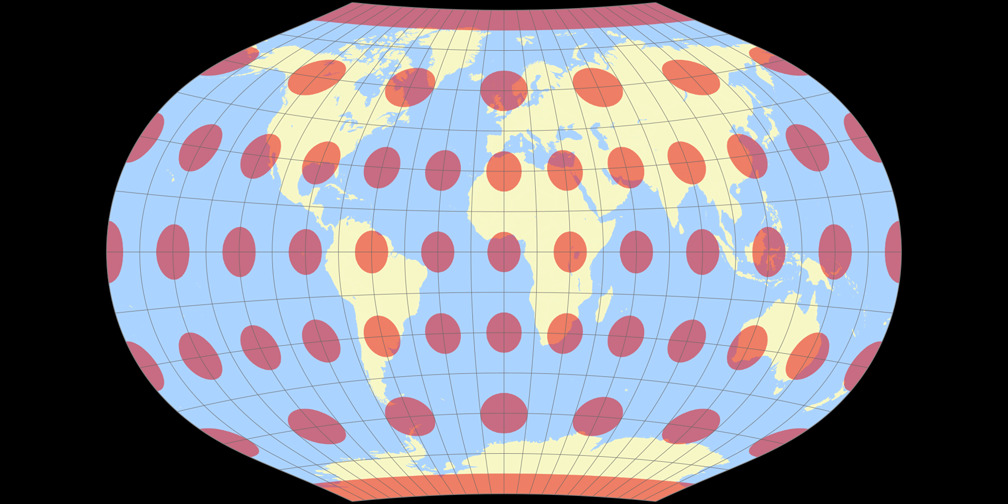
Rektangular, quadratisch
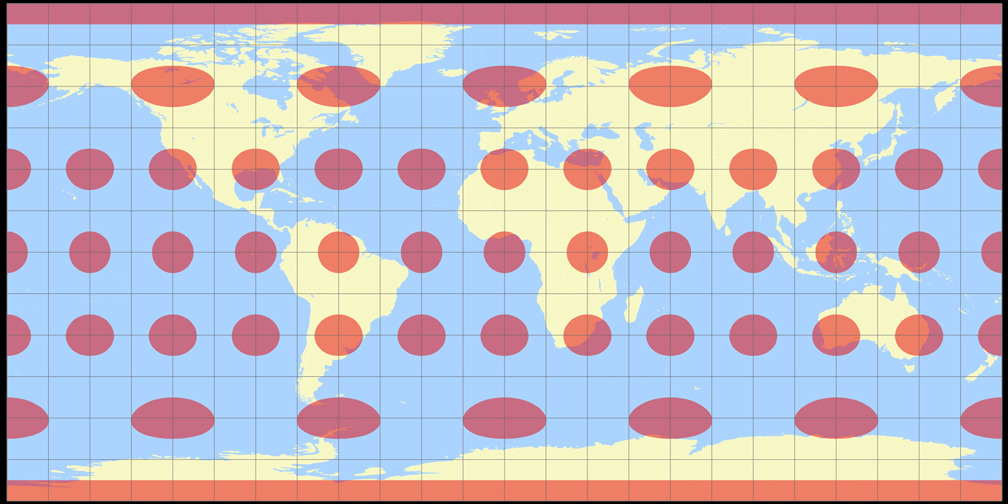
Ginzburg V Tissotsche Indikatrix c Tobias Jung
Rektangular, quadratisch Tissotsche Indikatrix c Tobias Jung
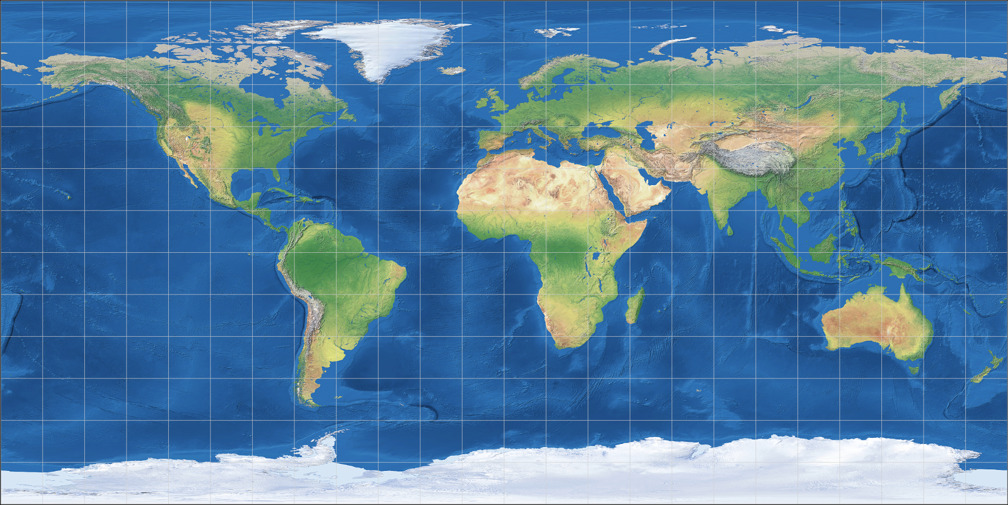
5. Vergleich: Physische Karte – auf gleiche Breite skaliert
Ginzburg V

Rektangular, quadratisch
6. Vergleich: Politische Karte – auf gleiche Breite skaliert
Ginzburg V
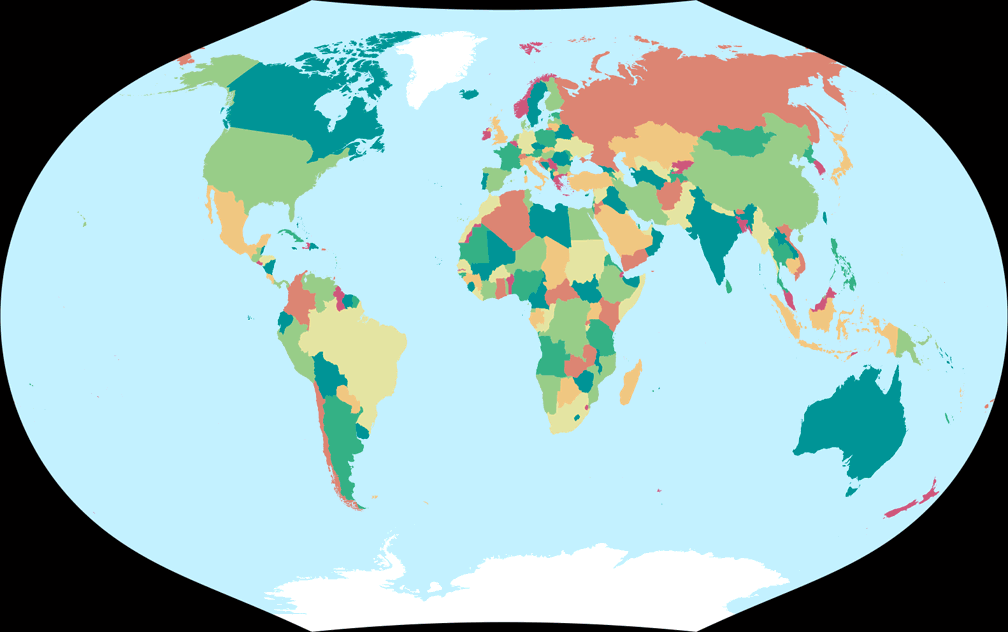
Rektangular, quadratisch

7. Vergleich: Umrisskarte – auf gleiche Breite skaliert

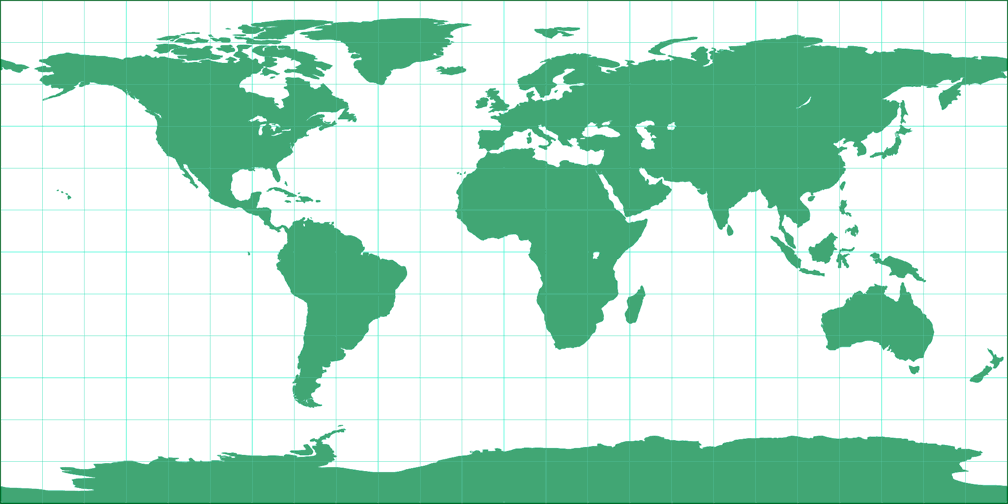
8. Vergleich: Tissotsche Indikatrix, 30° – auf gleiche Breite skaliert
Ginzburg V
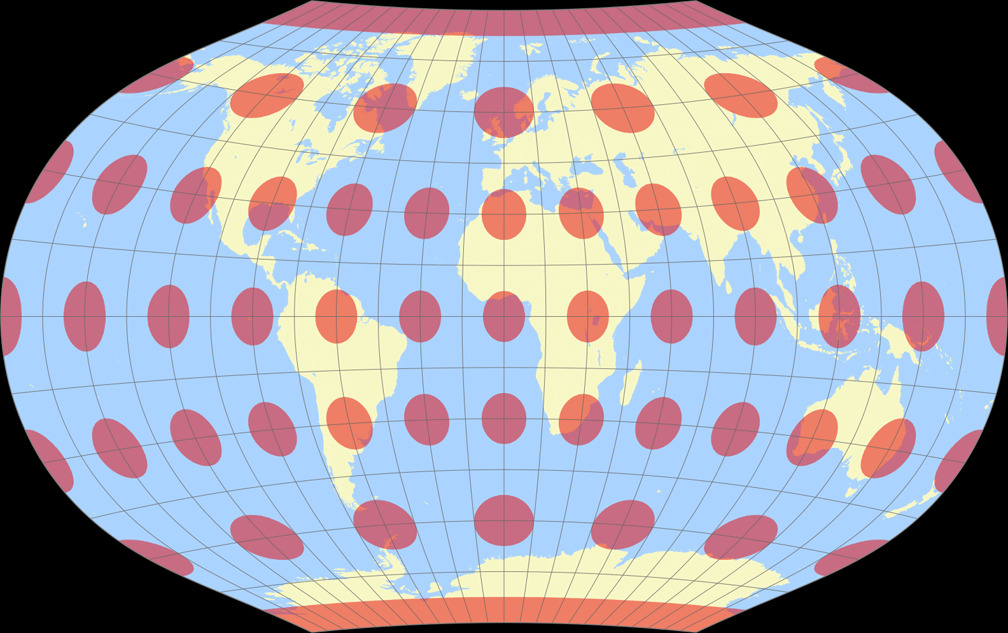
Rektangular, quadratisch
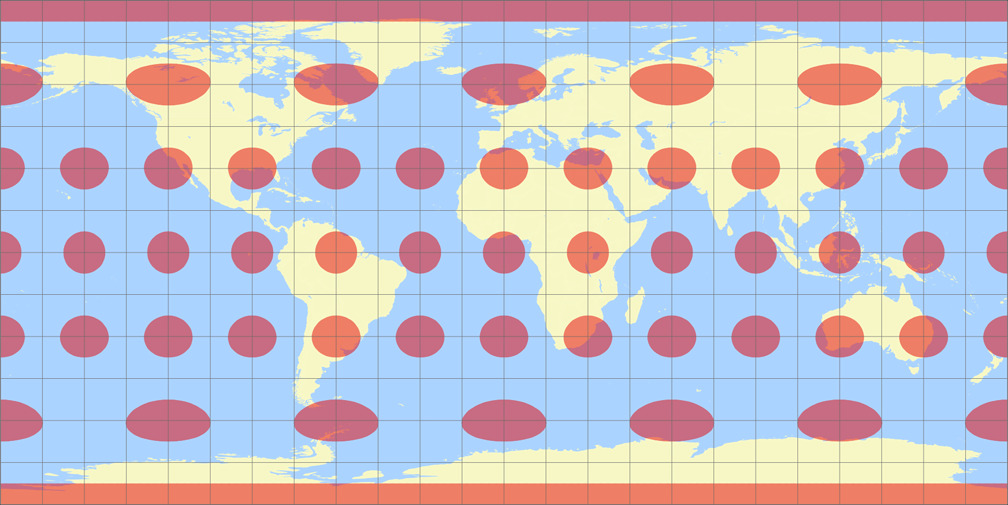
Ginzburg V Tissotsche Indikatrix c Tobias Jung
Rektangular, quadratisch Tissotsche Indikatrix c Tobias Jung
9. Vergleich: Tissotsche Indikatrix, 15° – passend skaliert
Ginzburg V
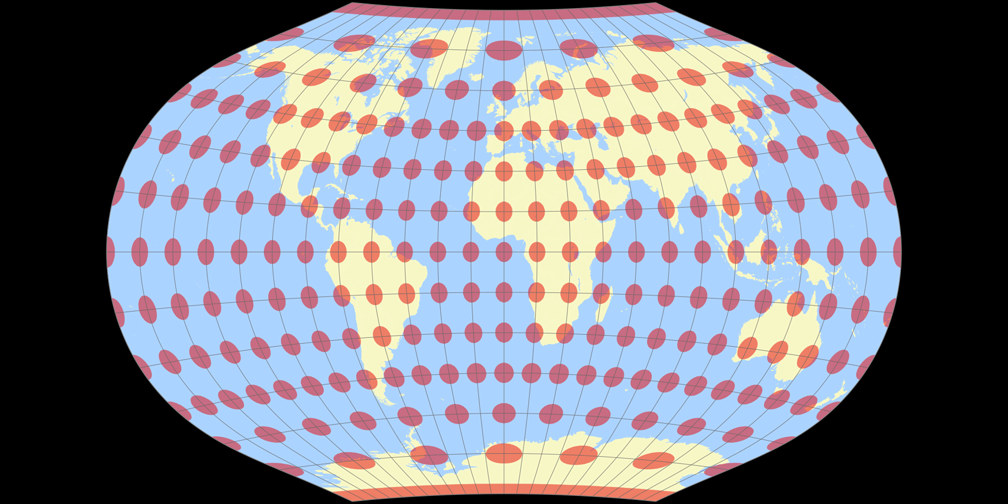
Rektangular, quadratisch
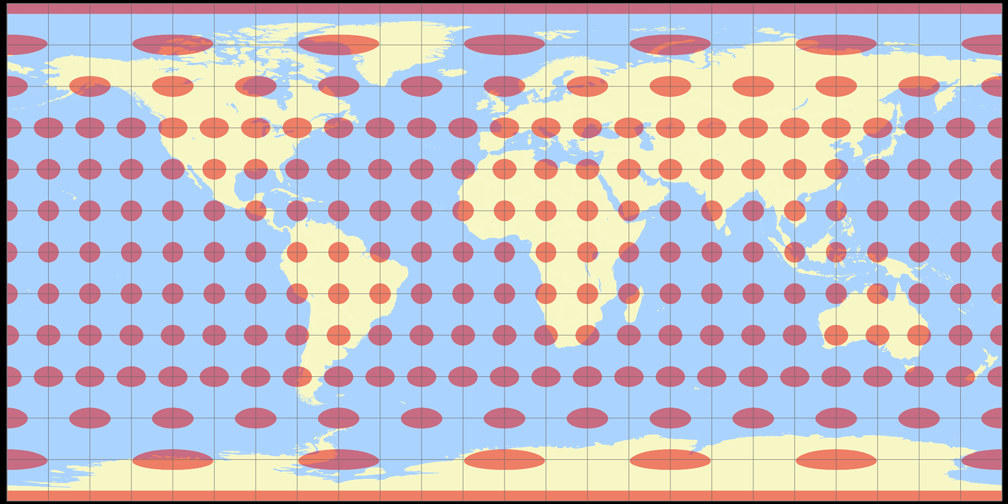
Ginzburg V Tissotsche Indikatrix c Tobias Jung
Rektangular, quadratisch Tissotsche Indikatrix c Tobias Jung
10. Vergleich: Tissotsche Indikatrix, 15° – auf gleiche Breite skaliert
Ginzburg V
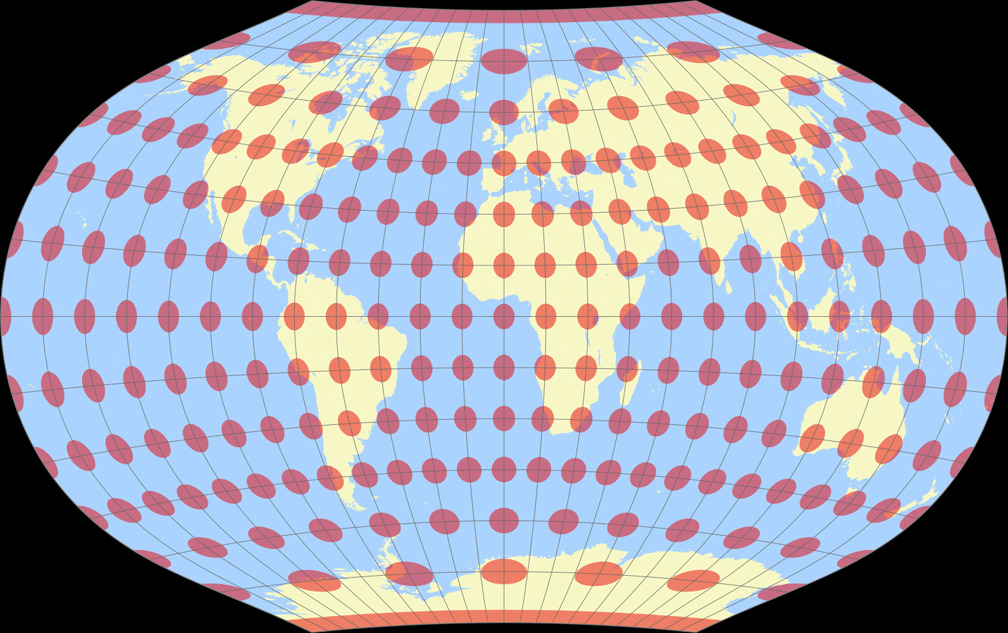
Rektangular, quadratisch
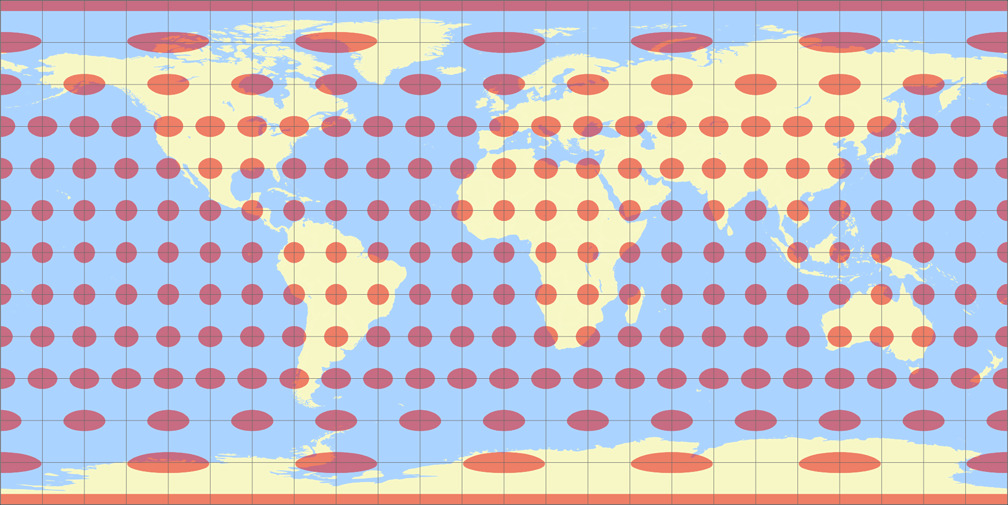
Ginzburg V Tissotsche Indikatrix c Tobias Jung
Rektangular, quadratisch Tissotsche Indikatrix c Tobias Jung