Kartenprojektionen vergleichen

Deutsch  •  English
—
[info]    Ansichtsoptionen:      

Meine Projektions-Kollektion:
Kartenprojektionen vergleichen

Rektangular, rechteckig (60°) vs. Toblers Abb. in einem Quadrat

Auswahlformular

Wähle die gewünschten Kartennetzentwürfe:

Netzentwurf 1:

Netzentwurf 2:

Vergleichsmodus:    [ Info ]

 

Oder:

→ Auswahl mit Vorschau-Bildern
→ Auswahl aus Liste

Infos zu den Netzentwürfen
  Rektangular, rechteckig (60°) Toblers Abb. in einem Quadrat
Urheber Marinus of Tyre (ca. 100 n.Chr.) Waldo Tobler (1993)
Gruppe Zylinder Zylinder
Eigenschaft Längentreu Flächentreu
Andere Namen
  • Rechteckige Plattkarte (und ja, es ist immer noch die rechteckige Plattkarte, auch wenn das Ergebnis quadratisch ist)
  • Toblers flächentreue Erdabbildung in einem Quadrat
Anm.Anmerkungen Hier: 60° Nord/Süd als Schnittparallele, um eine exakt quadratische Karte zu erstellen.

Ich habe diese spezielle Konfiguration im März 2020 hinzugefügt. Ich habe sie noch nie gesehen, aber es ist nicht unwahrscheinlich, dass sie irgendjemand irgendwo schon einmal benutzt hat.		 Flächentreue zylindrische Projektion mit Standardparallelen auf 55°39′14″ (= 55,65389°) Nord/Süd, was in einer genau quadratischen Projektion resultiert.
Empfohlene Vergleiche Toblers Abb. in einem Quadrat Rektangular, rechteckig (60°)
Diese Paarung gehört zur Liste der empfohlenen Vergleiche – aber warum?
Um den Unterschied zwischen einer quadratischen flächentreuen Projektion und einer quadratischen Projektion mit gleichabständigen Breitenkreisen zu zeigen.

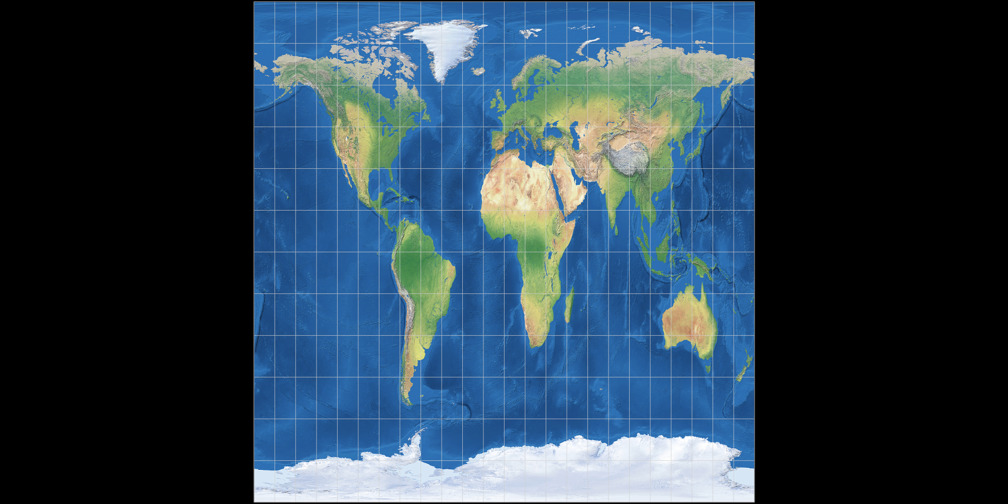
1. Vergleich: Physische Karte – passend skaliert

Rektangular, rechteckig (60°)
Rektangular, rechteckig (60°)
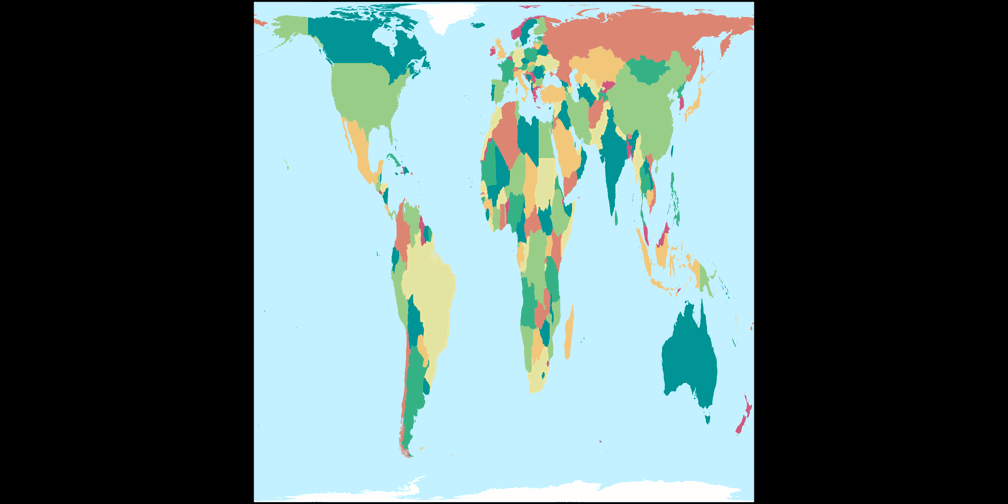
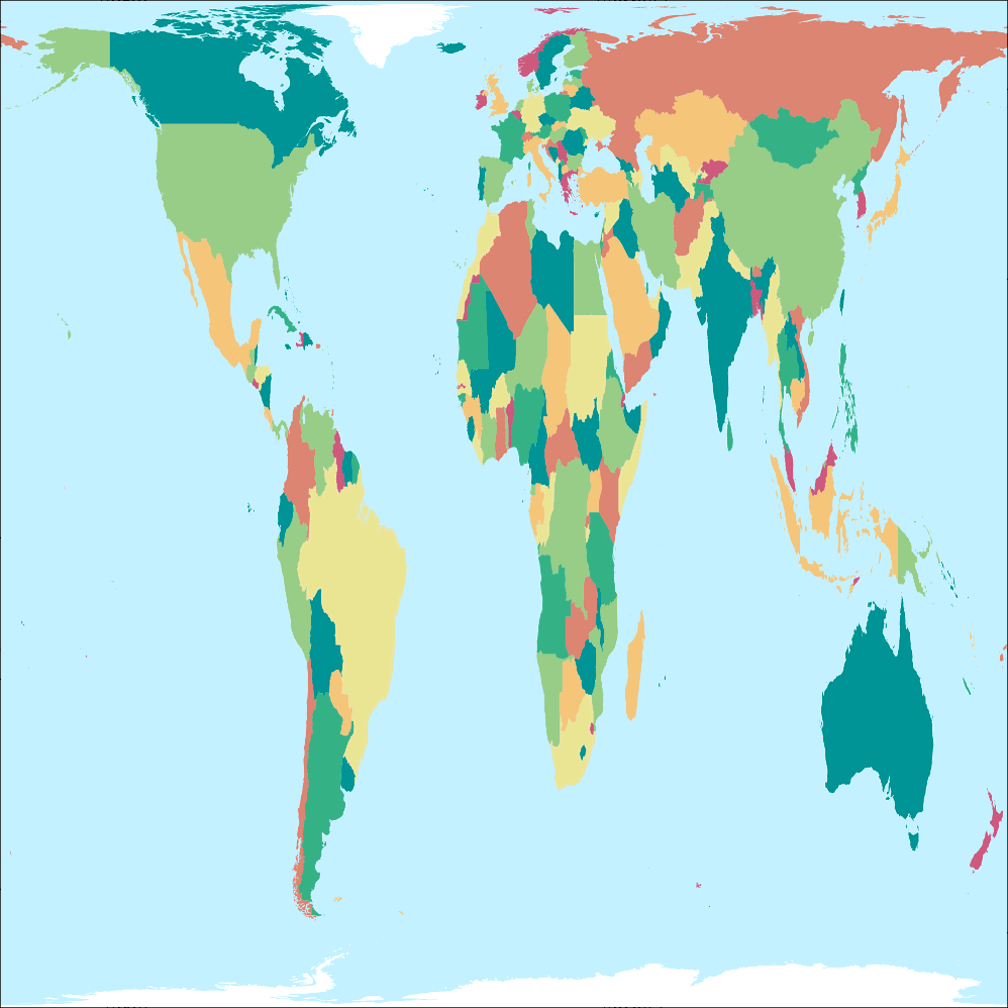
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat
Rektangular, rechteckig (60°) c Tobias Jung     Toblers Abb. in einem Quadrat c Tobias Jung

2. Vergleich: Politische Karte – passend skaliert

Rektangular, rechteckig (60°)
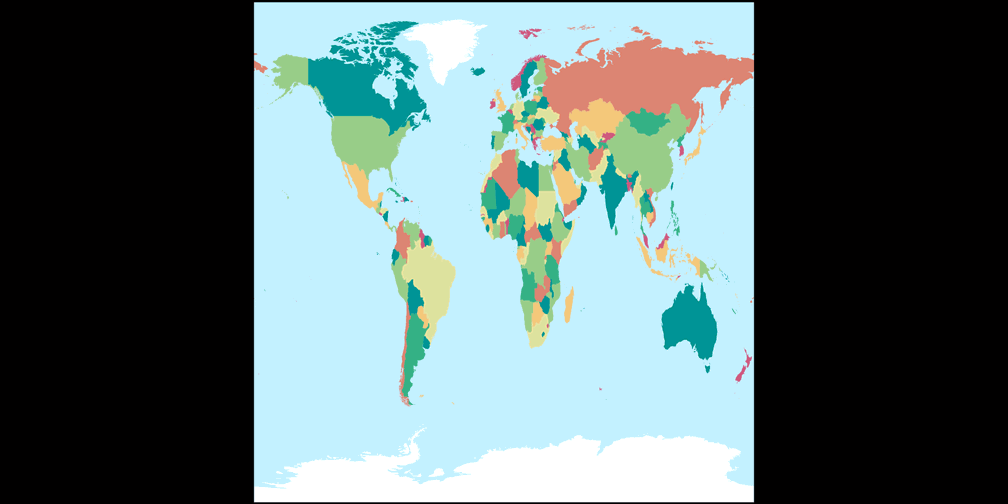
Rektangular, rechteckig (60°)
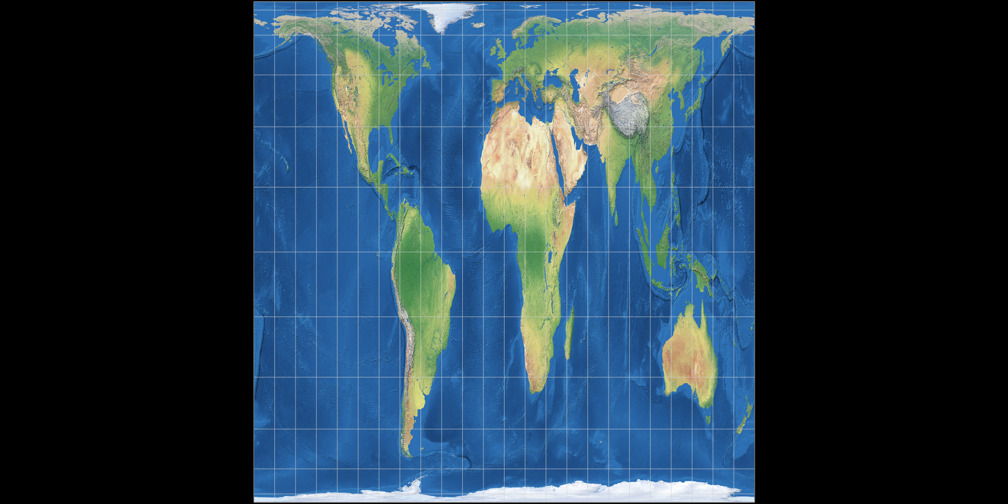
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat
Rektangular, rechteckig (60°) c Tobias Jung     Toblers Abb. in einem Quadrat c Tobias Jung

3. Vergleich: Umrisskarte – passend skaliert

Klick auf den Namen blendet die Grafik ein und aus
Graue Flächen: Überlagerung der Entwürfe
Rektangular, rechteckig (60°) Umrisskarte
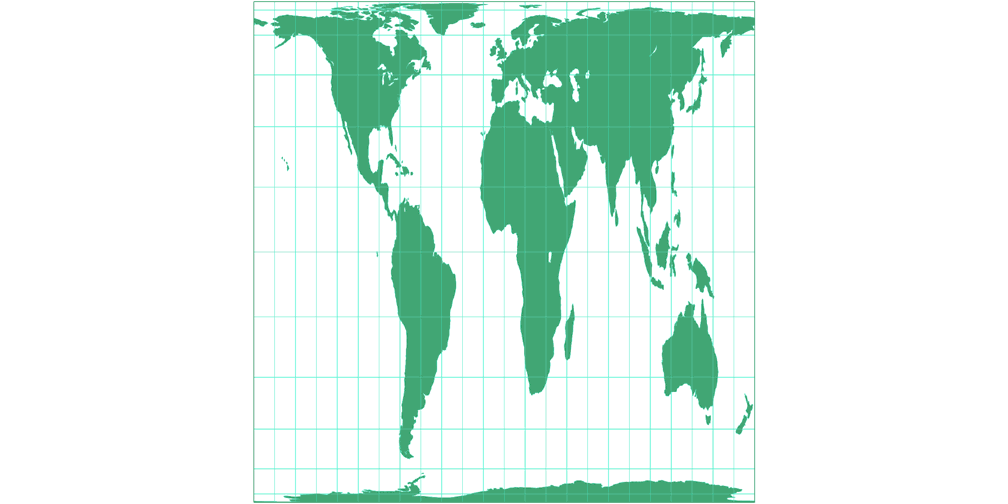
Toblers Abb. in einem Quadrat Umrisskarte
Rektangular, rechteckig (60°) Umrisskarte c Tobias Jung     Toblers Abb. in einem Quadrat Umrisskarte c Tobias Jung

4. Vergleich: Tissotsche Indikatrix, 30° – passend skaliert

Rektangular, rechteckig (60°)
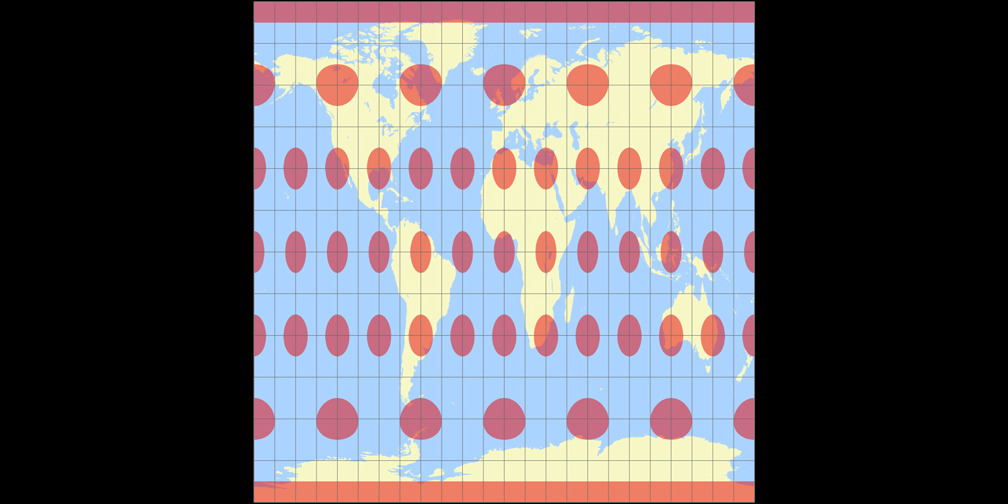
Rektangular, rechteckig (60°) Tissotsche Indikatrix
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat Tissotsche Indikatrix
Rektangular, rechteckig (60°) Tissotsche Indikatrix c Tobias Jung     Toblers Abb. in einem Quadrat Tissotsche Indikatrix c Tobias Jung

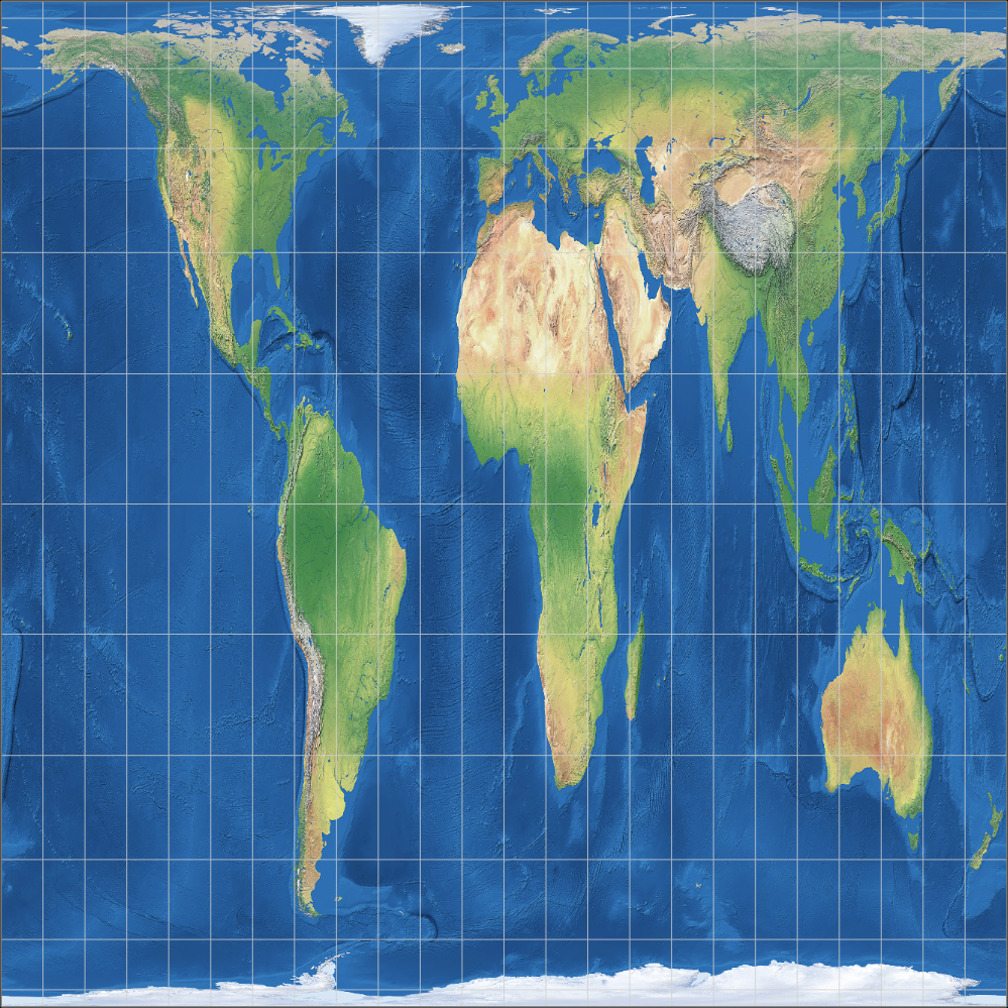
5. Vergleich: Physische Karte – auf gleiche Breite skaliert

Rektangular, rechteckig (60°)
Rektangular, rechteckig (60°)
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat
Rektangular, rechteckig (60°) c Tobias Jung     Toblers Abb. in einem Quadrat c Tobias Jung

6. Vergleich: Politische Karte – auf gleiche Breite skaliert

Rektangular, rechteckig (60°)
Rektangular, rechteckig (60°)
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat
Rektangular, rechteckig (60°) c Tobias Jung     Toblers Abb. in einem Quadrat c Tobias Jung

7. Vergleich: Umrisskarte – auf gleiche Breite skaliert

Klick auf den Namen blendet die Grafik ein und aus
Graue Flächen: Überlagerung der Entwürfe
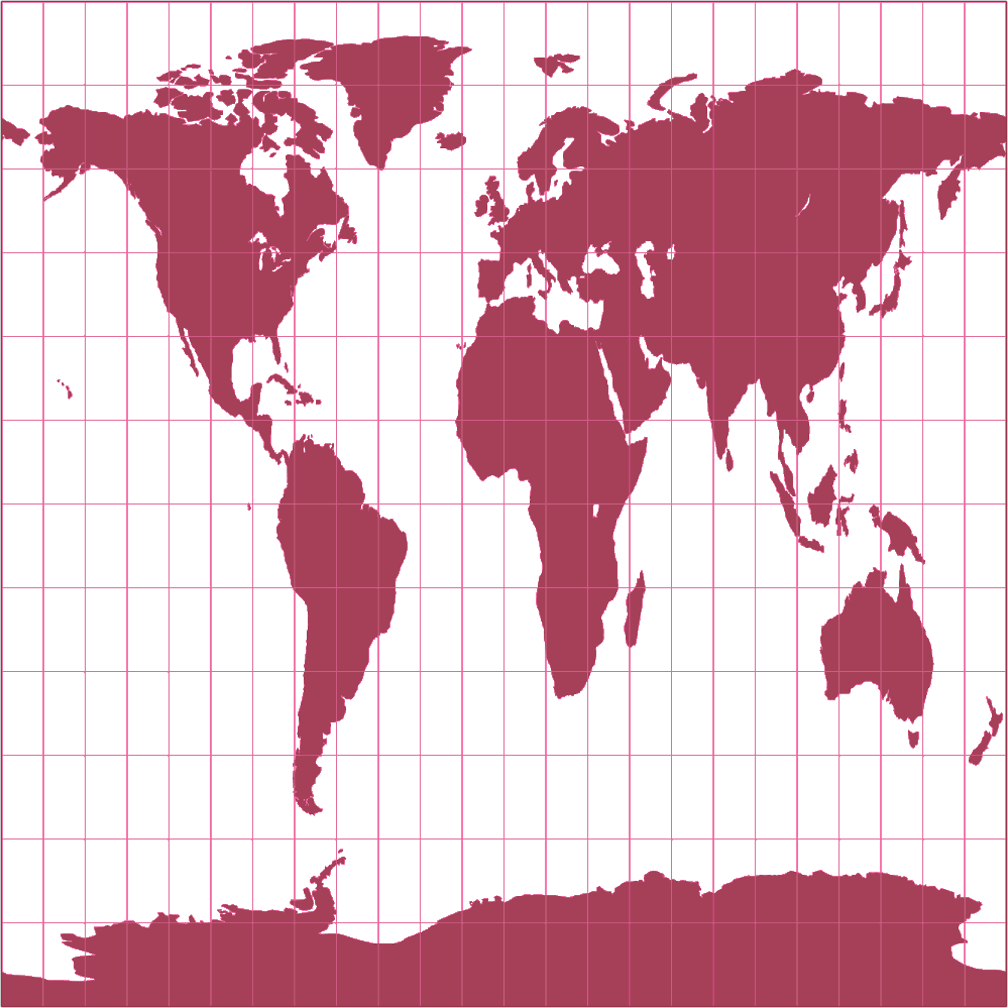
Rektangular, rechteckig (60°) Umrisskarte
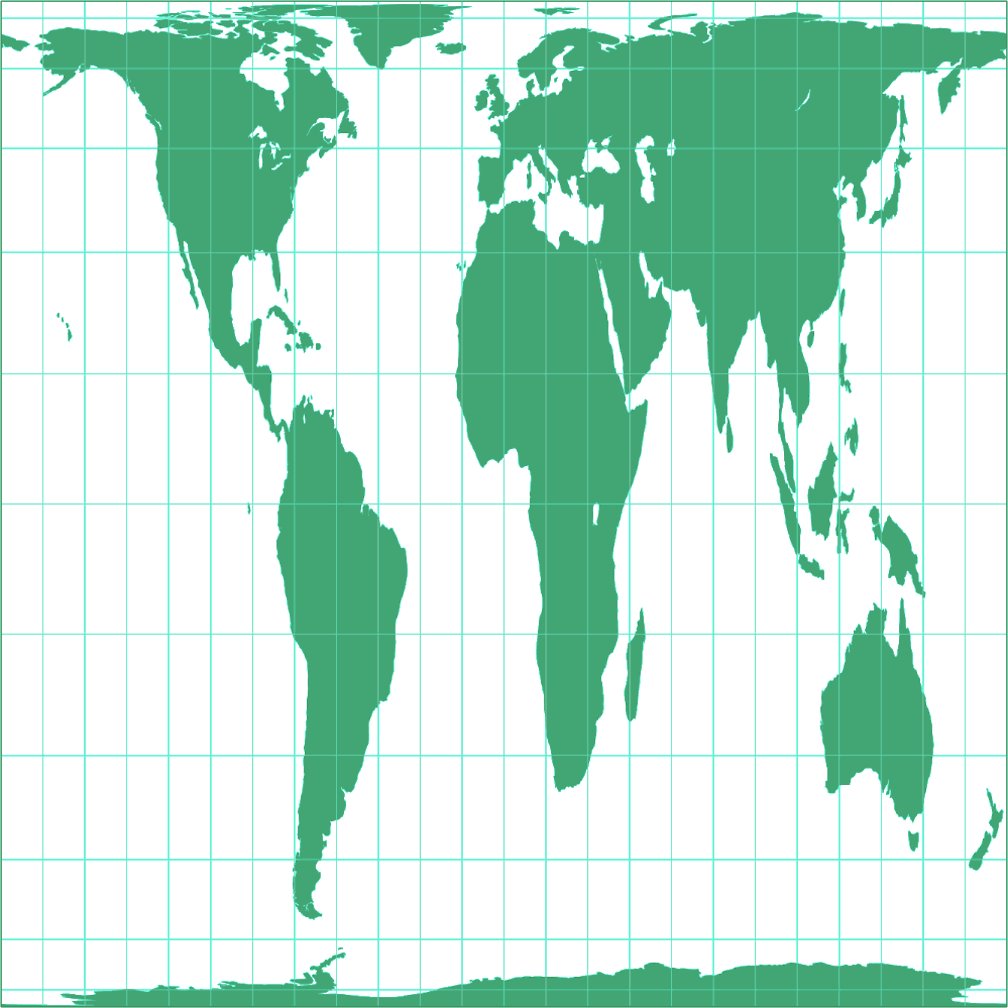
Toblers Abb. in einem Quadrat Umrisskarte
Rektangular, rechteckig (60°) Umrisskarte c Tobias Jung     Toblers Abb. in einem Quadrat Umrisskarte c Tobias Jung

8. Vergleich: Tissotsche Indikatrix, 30° – auf gleiche Breite skaliert

Rektangular, rechteckig (60°)
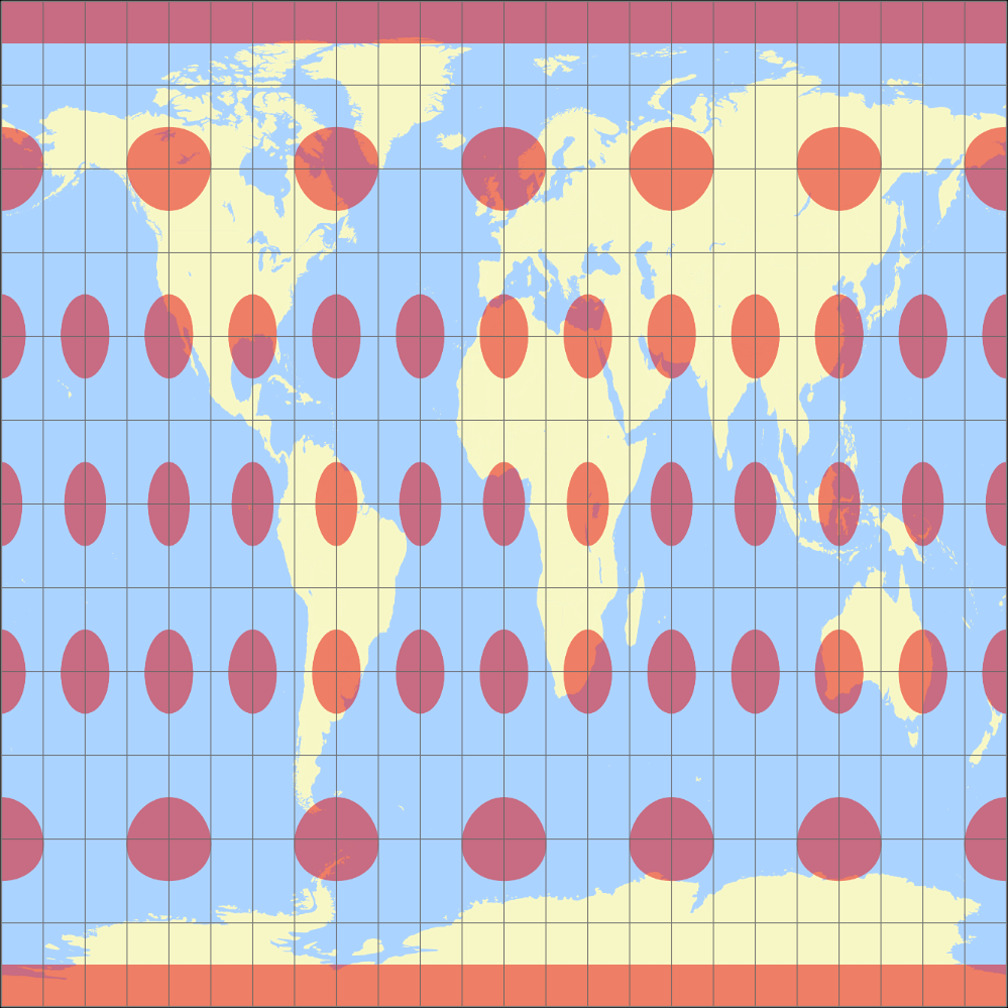
Rektangular, rechteckig (60°) Tissotsche Indikatrix
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat Tissotsche Indikatrix
Rektangular, rechteckig (60°) Tissotsche Indikatrix c Tobias Jung     Toblers Abb. in einem Quadrat Tissotsche Indikatrix c Tobias Jung

9. Vergleich: Tissotsche Indikatrix, 15° – passend skaliert

Rektangular, rechteckig (60°)
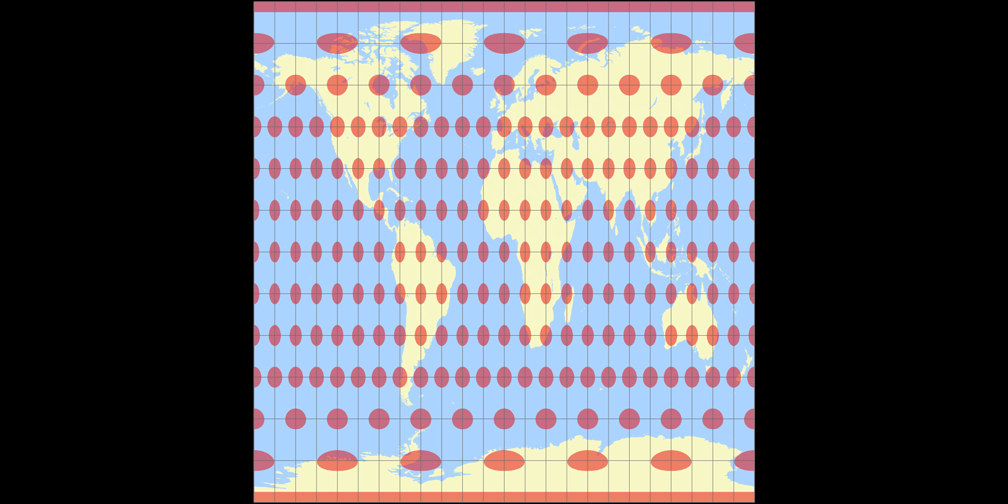
Rektangular, rechteckig (60°) Tissotsche Indikatrix
Toblers Abb. in einem Quadrat
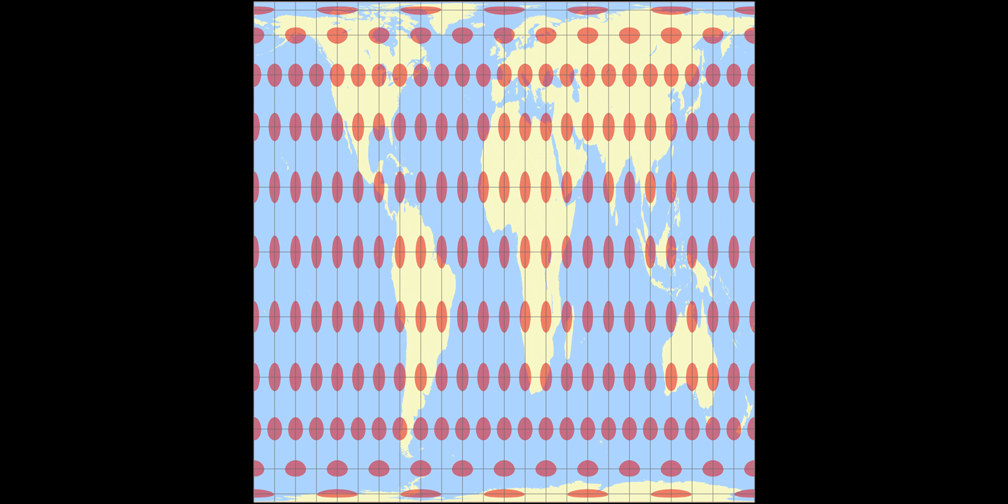
Toblers Abb. in einem Quadrat Tissotsche Indikatrix
Rektangular, rechteckig (60°) Tissotsche Indikatrix c Tobias Jung     Toblers Abb. in einem Quadrat Tissotsche Indikatrix c Tobias Jung

10. Vergleich: Tissotsche Indikatrix, 15° – auf gleiche Breite skaliert

Rektangular, rechteckig (60°)
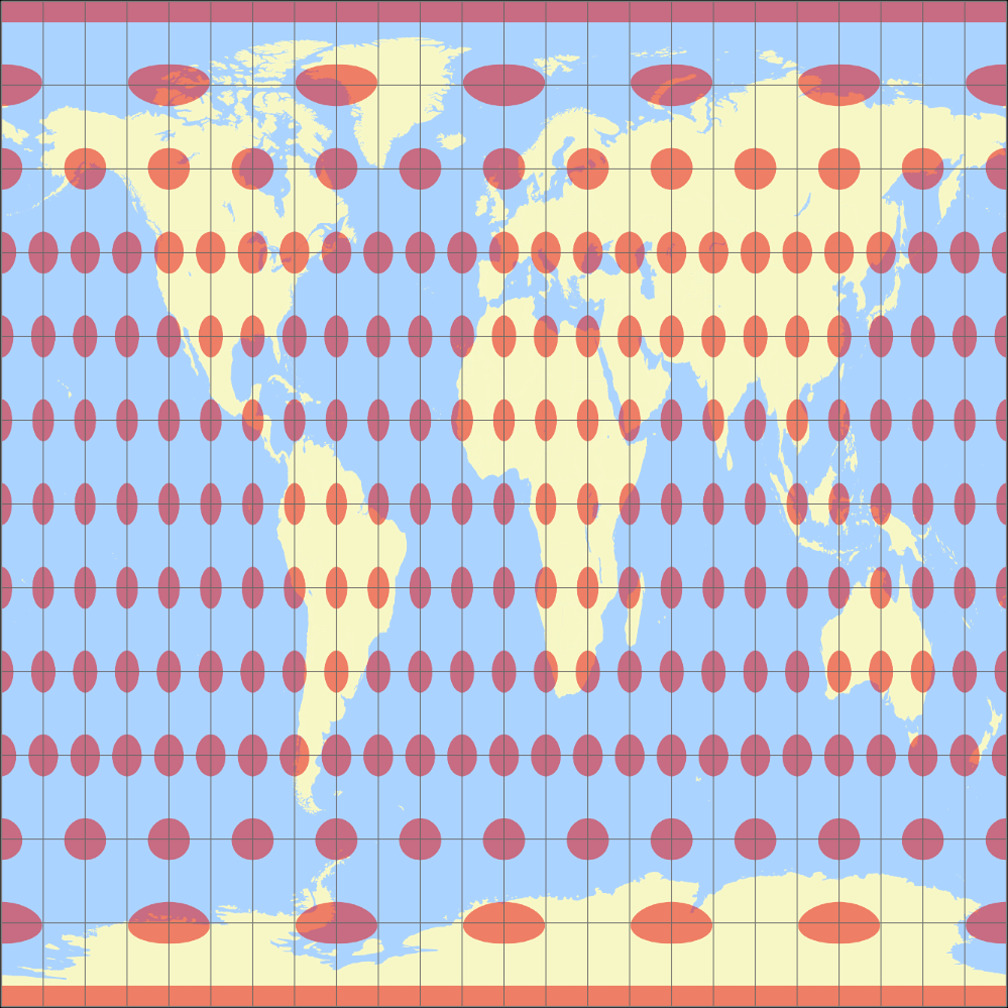
Rektangular, rechteckig (60°) Tissotsche Indikatrix
Toblers Abb. in einem Quadrat
Toblers Abb. in einem Quadrat Tissotsche Indikatrix
Rektangular, rechteckig (60°) Tissotsche Indikatrix c Tobias Jung     Toblers Abb. in einem Quadrat Tissotsche Indikatrix c Tobias Jung
 

Nach oben