Meine Projektions-Kollektion:
Kartenprojektionen vergleichen
Winkel II vs. Winkel-Denner III (50,46°)
| Winkel II | Winkel-Denner III (50,46°) | |
|---|---|---|
| Urheber | Oswald Winkel (1921) | Peter Denner (2023) |
| Gruppe | Pseudozylinder | Lentikulär |
| Eigenschaft | Vermittelnd | Vermittelnd |
| Andere Namen | — |
|
| Anm.Anmerkungen | — | Arithmetisches Mittel der Rektangular- (mit φ0 ≈ 50°28´) und der Aitoff-Projektion für die x-Werte, unter Verwendung der Aitoff-Projektion (ohne Mittelung) für die y-Werte. Ursprünglich in einem Thread des mapthematics-Forums (engl.) vorgestellt. Siehe auch den Blogpost Die Winkel-Denner-Projektionen. |
| Empfohlene Vergleiche | — | — |
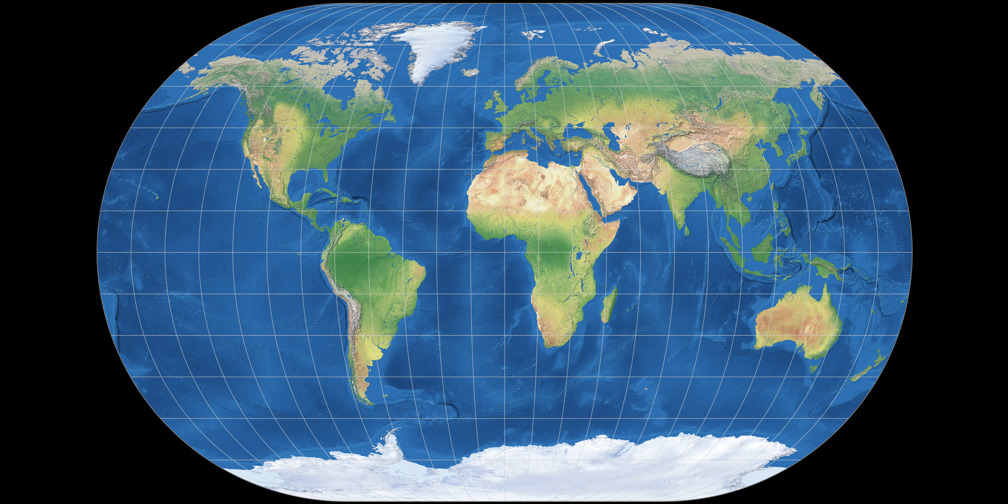
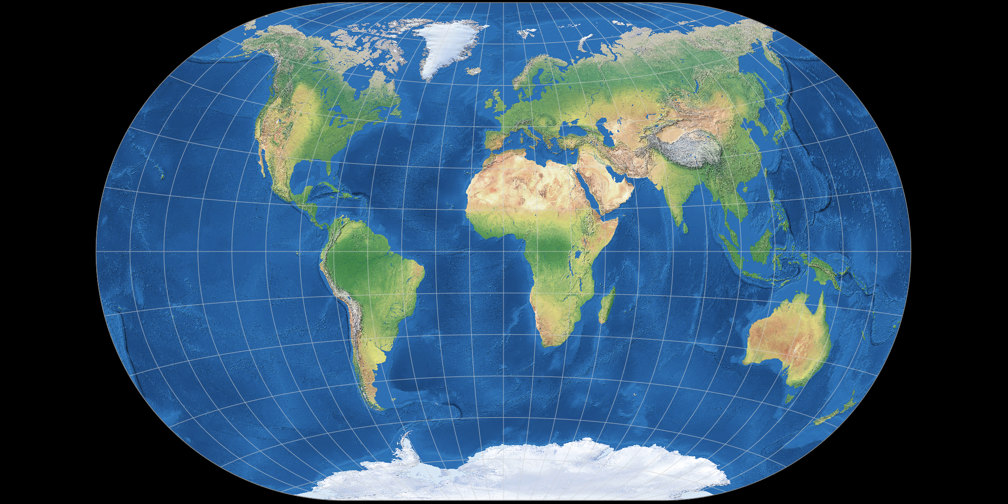
1. Vergleich: Physische Karte – passend skaliert
2. Vergleich: Politische Karte – passend skaliert
Winkel II
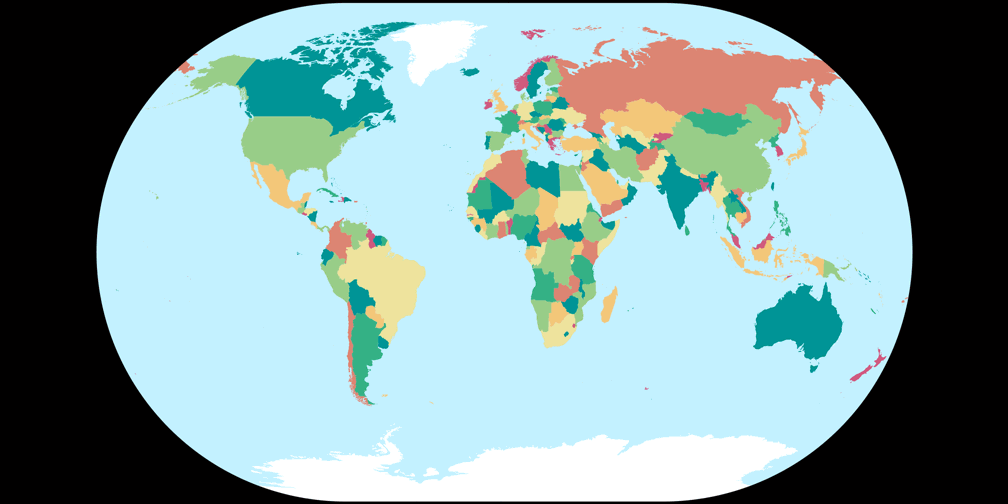
Winkel-Denner III (50,46°)

3. Vergleich: Umrisskarte – passend skaliert
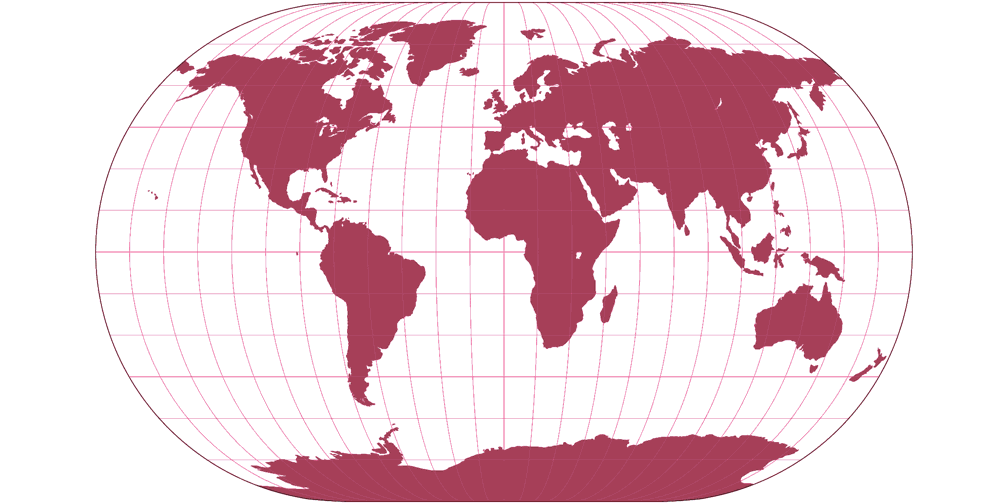
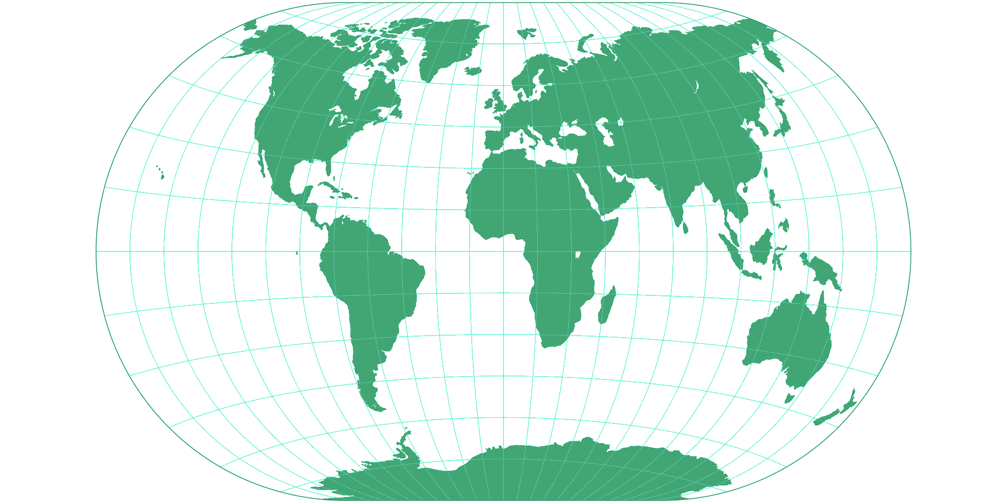
4. Vergleich: Tissotsche Indikatrix, 30° – passend skaliert
Winkel II
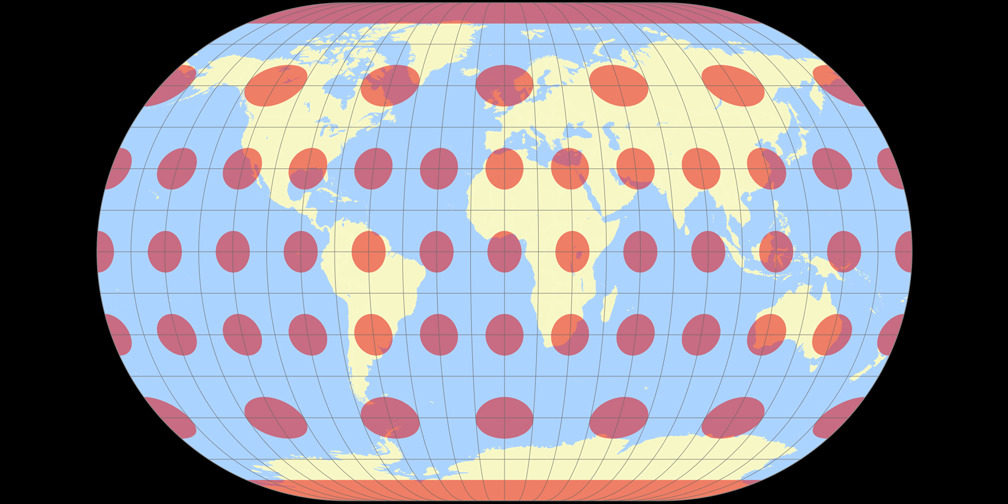
Winkel-Denner III (50,46°)
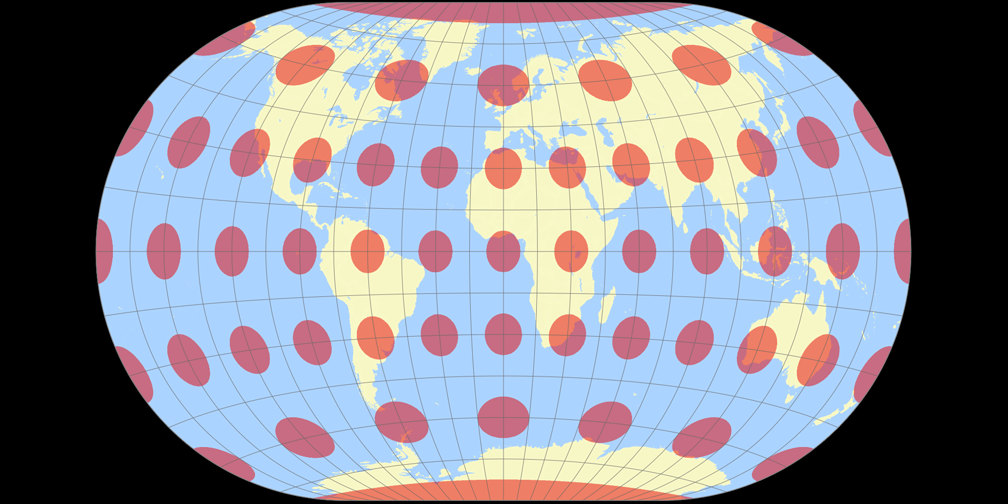
Winkel II Tissotsche Indikatrix c Tobias Jung
Winkel-Denner III (50,46°) Tissotsche Indikatrix c Tobias Jung
5. Vergleich: Physische Karte – auf gleiche Breite skaliert
Winkel II
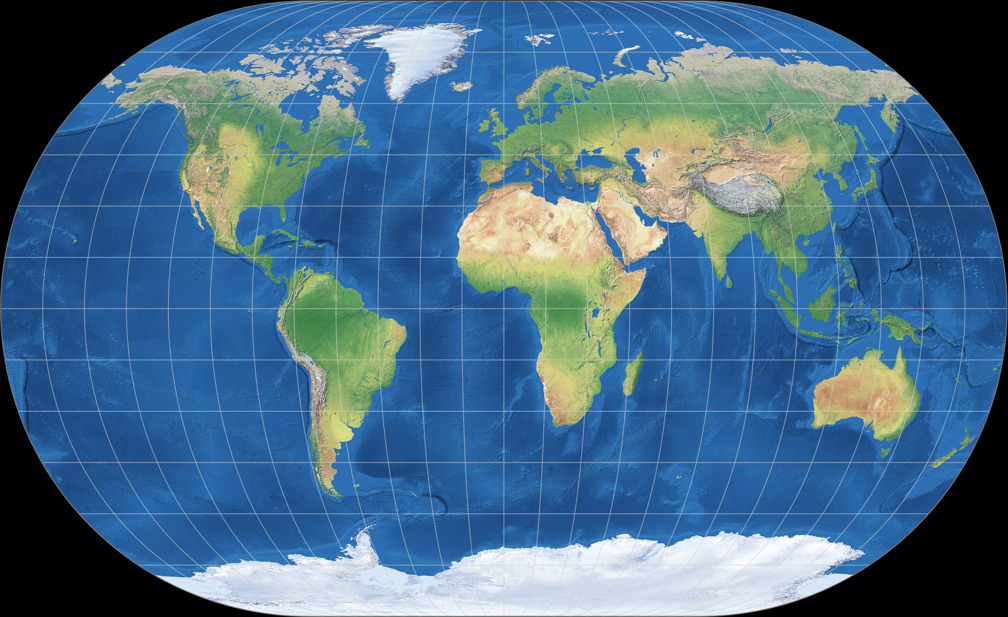
Winkel-Denner III (50,46°)
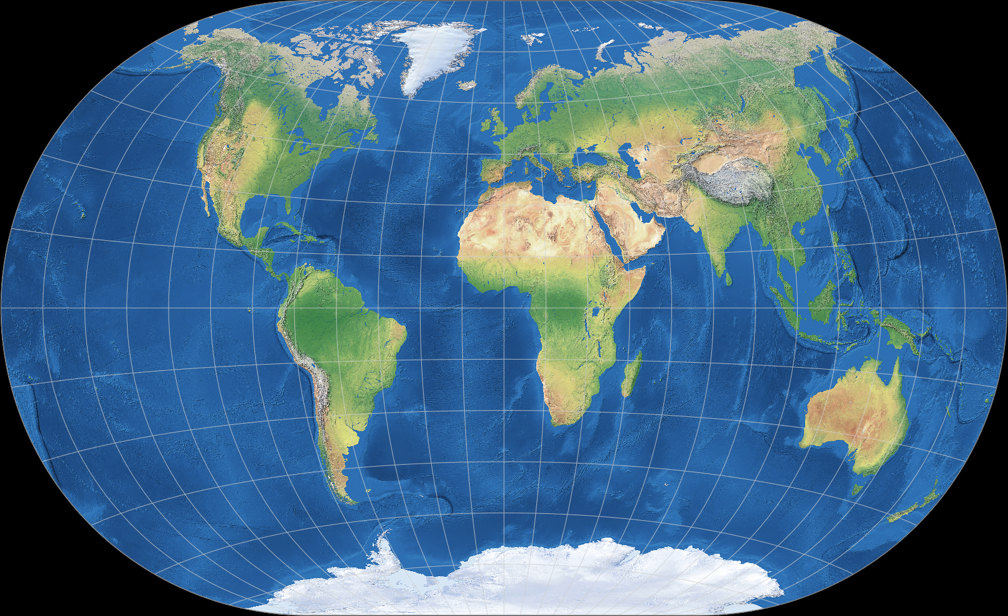
6. Vergleich: Politische Karte – auf gleiche Breite skaliert
Winkel II
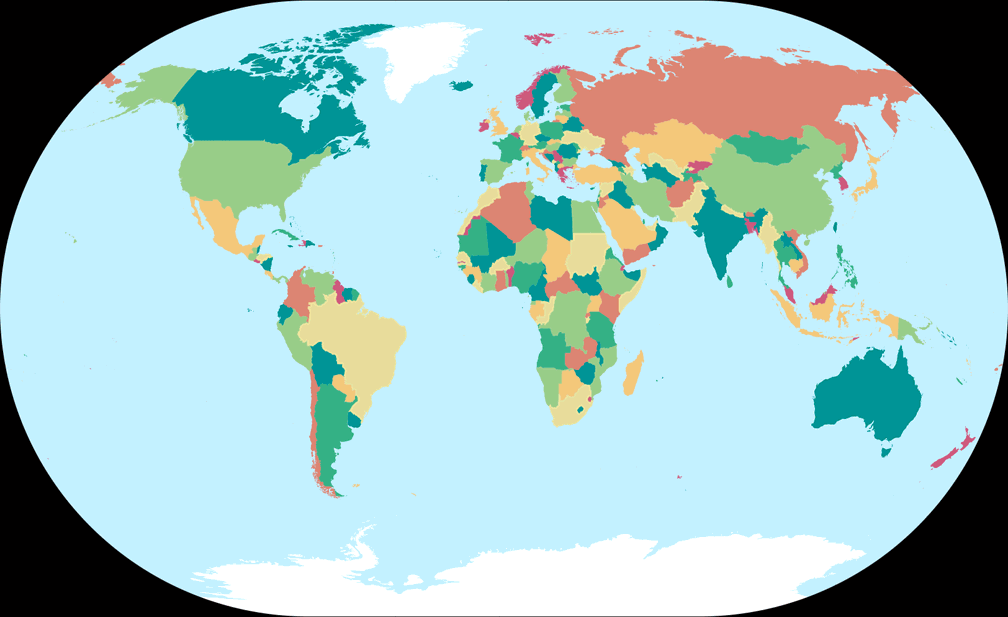
Winkel-Denner III (50,46°)
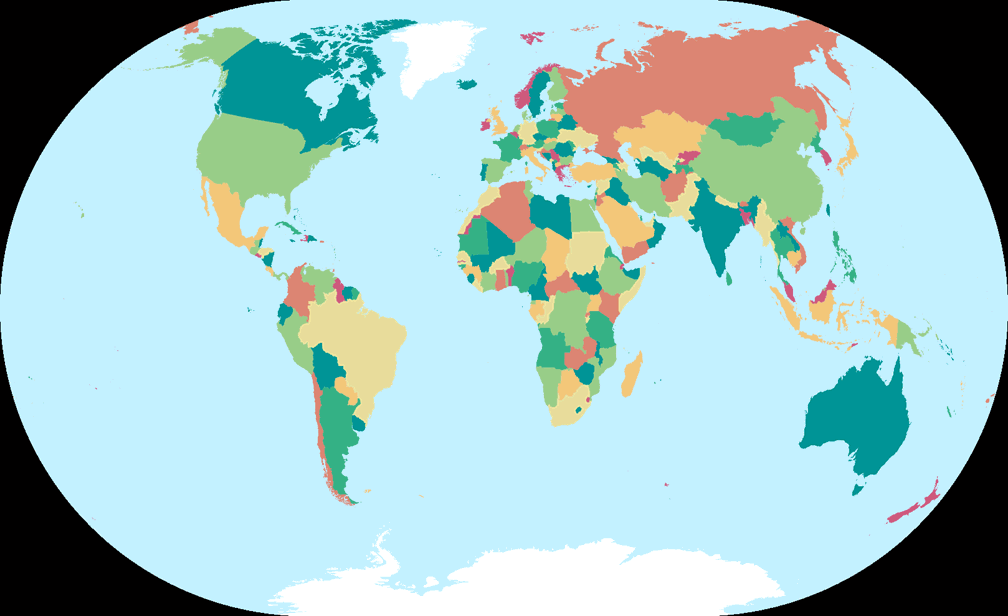
7. Vergleich: Umrisskarte – auf gleiche Breite skaliert
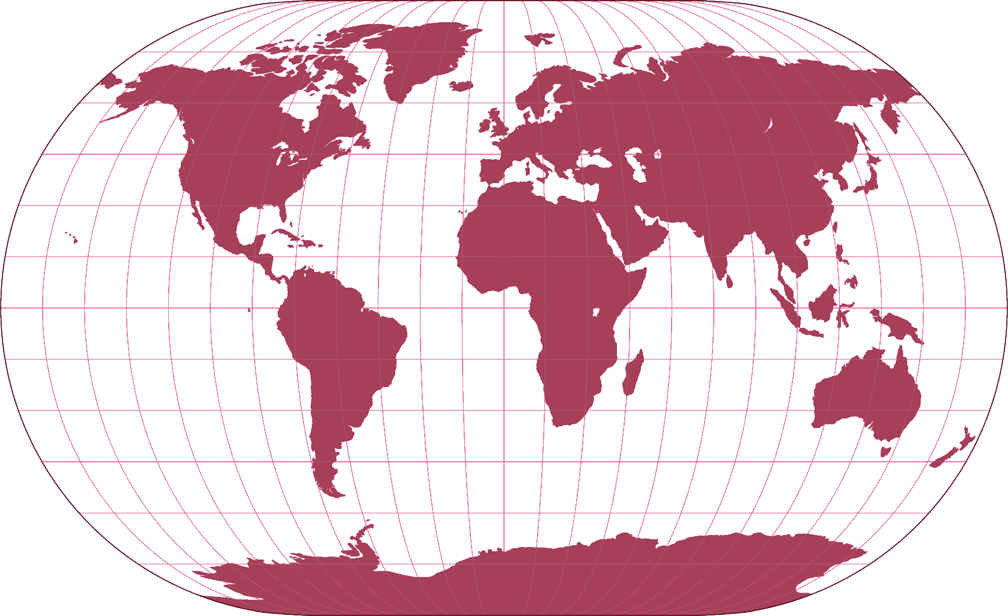
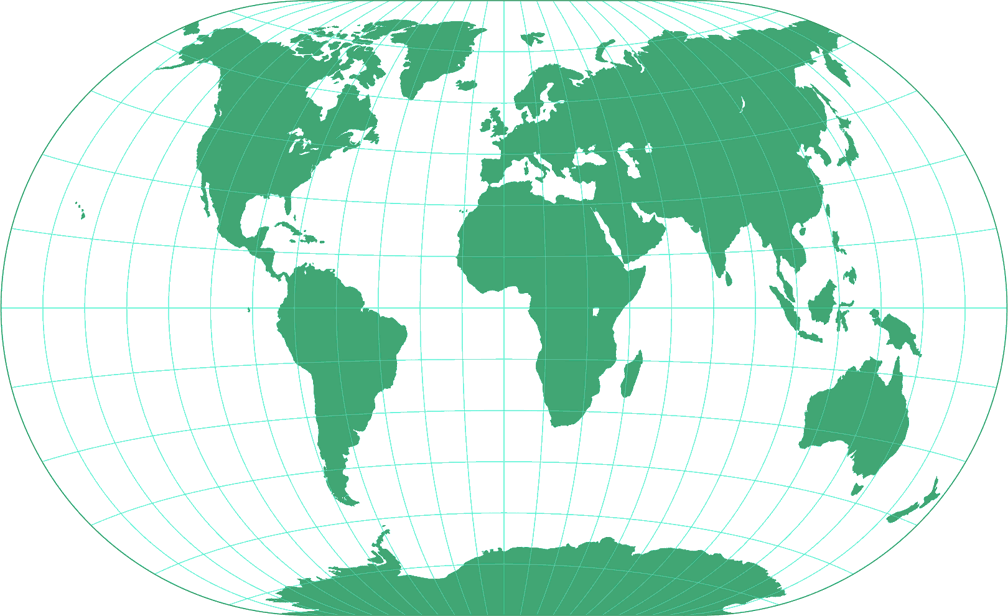
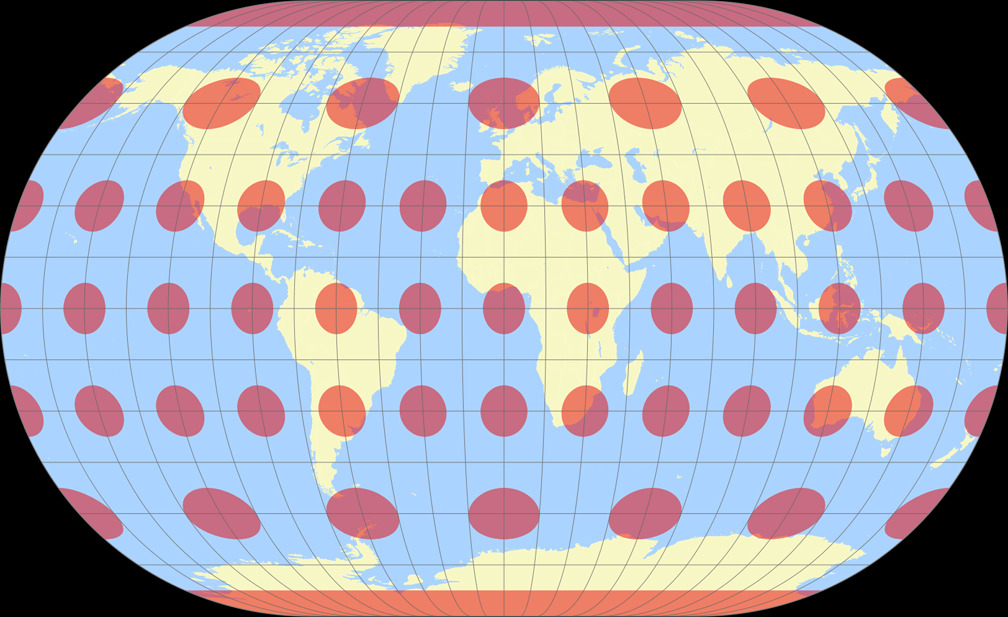
8. Vergleich: Tissotsche Indikatrix, 30° – auf gleiche Breite skaliert
Winkel II
Winkel-Denner III (50,46°)
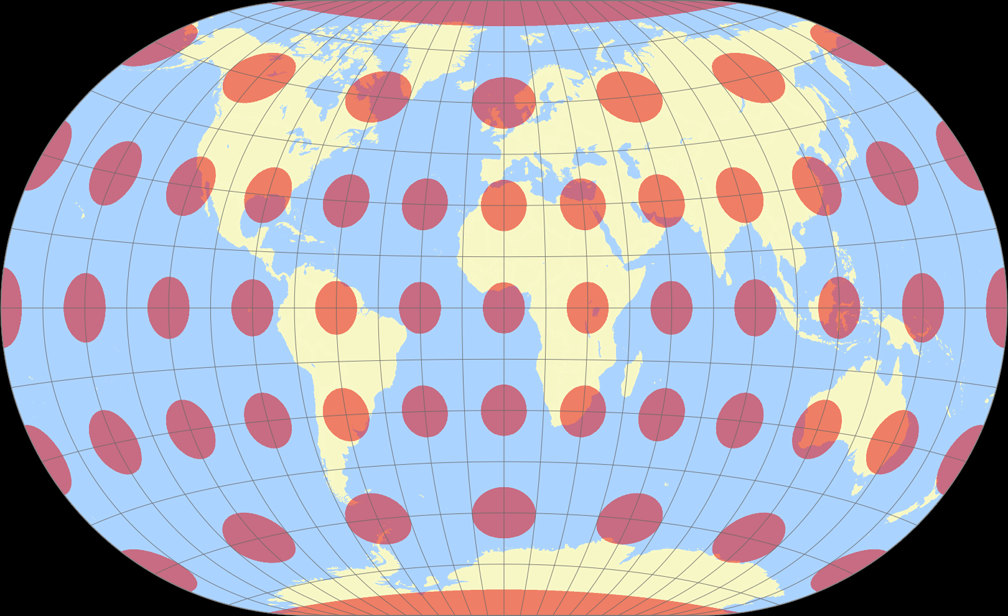
Winkel II Tissotsche Indikatrix c Tobias Jung
Winkel-Denner III (50,46°) Tissotsche Indikatrix c Tobias Jung
9. Vergleich: Tissotsche Indikatrix, 15° – passend skaliert
Winkel II
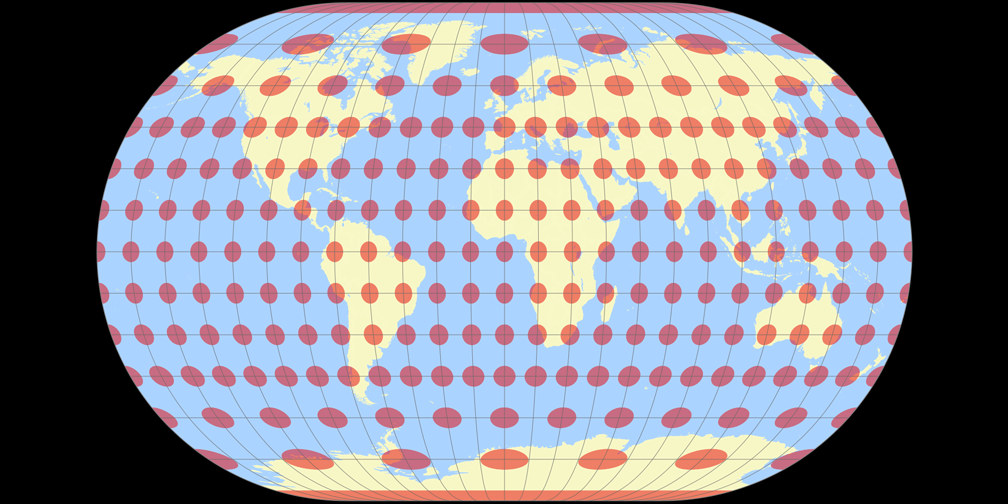
Winkel-Denner III (50,46°)

Winkel II Tissotsche Indikatrix c Tobias Jung
Winkel-Denner III (50,46°) Tissotsche Indikatrix c Tobias Jung
10. Vergleich: Tissotsche Indikatrix, 15° – auf gleiche Breite skaliert
Winkel II
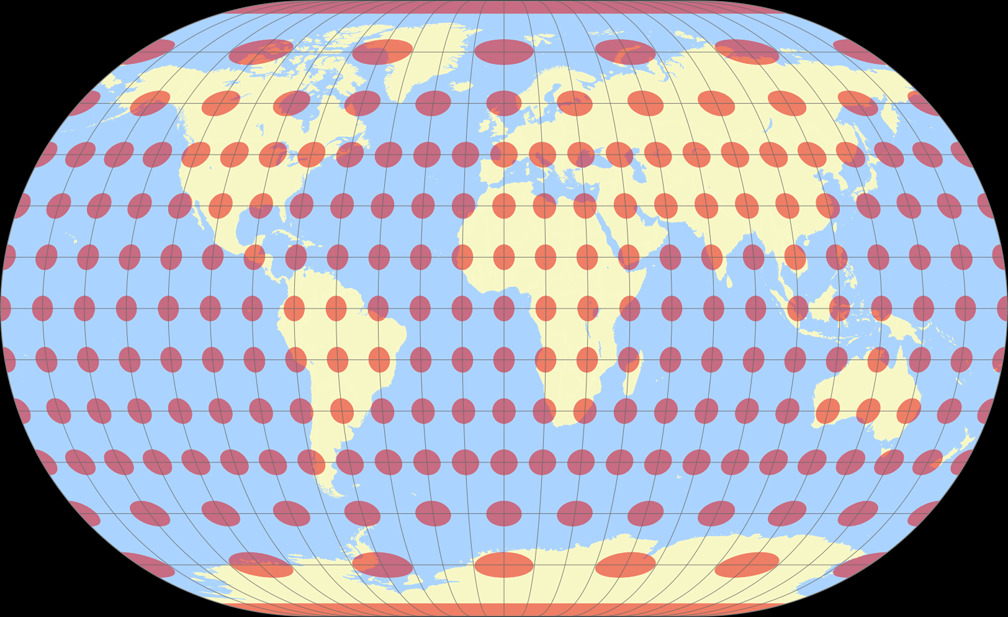
Winkel-Denner III (50,46°)
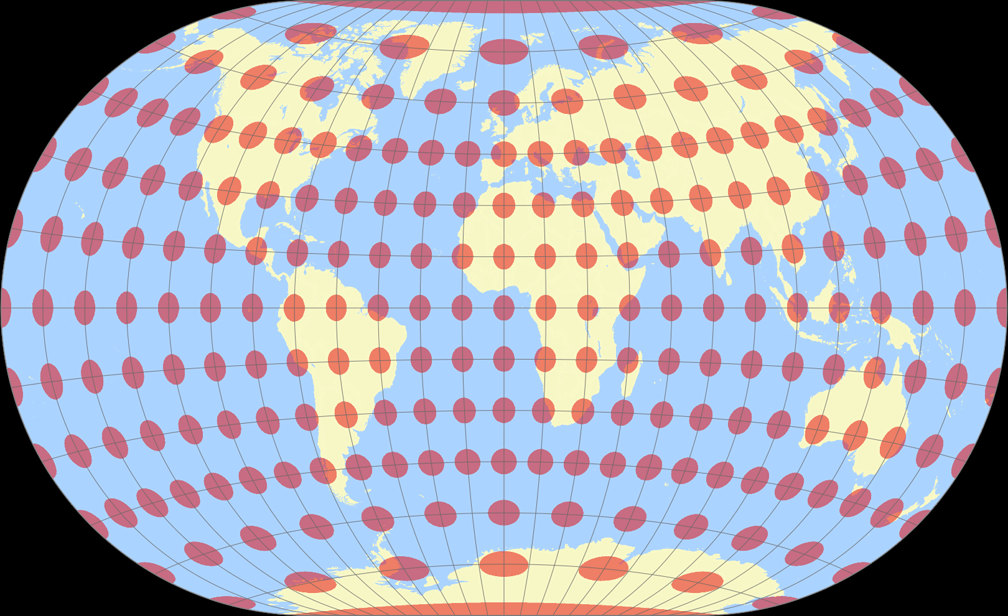
Winkel II Tissotsche Indikatrix c Tobias Jung
Winkel-Denner III (50,46°) Tissotsche Indikatrix c Tobias Jung