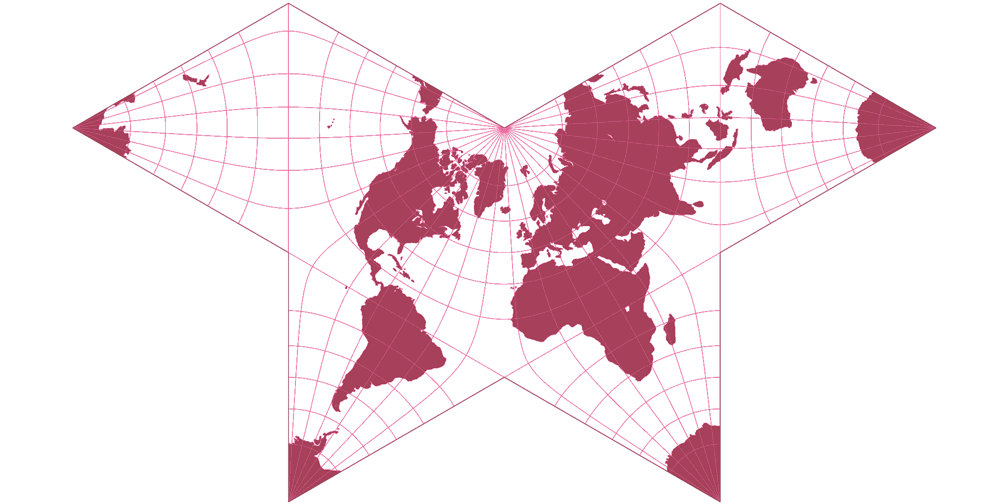
Cahills konformer Schmetterling
| Cahills konformer Schmetterling | |
|---|---|
| Urheber | Bernard J. S. Cahill, Oscar S. Adams (ca. 1929) |
| Gruppe | Polyedrische |
| Eigenschaft | Winkeltreu |
| Andere Namen | — |
| Anm.Anmerkungen | Cahill entwickelte 1909 seine erste (vermittelnde) Karte in Schmetterlingsform. Auf Cahills Anregung entwickelte Oscar S. Adams Mitte der 1920er Jahre die mathematischen Formeln für die hier gezeigte winkeltreue Variante, welche Cahill 1929 veröffentlichte. In Cahills originalem Arrangement wurde Afrika in den oberen linken »Flügel« gelegt, zur besseren Vergleichbarkeit wurde die hier gezeigte Karte auf 20° West zentriert. Siehe auch Vier winkeltreue polyedrische Projektionen und mehr. |
Zeige andere Darstellungen dieser Projektion:
Angaben in [eckigen Klammern] zeigen die Größe der eigentlichen Projektion
(abzüglich des schwarzen oder weißen Rahmens).
Wenn mit [≈] markiert, ist die Größe mit und
ohne Ramen in etwa gleich.