Kartenprojektionen vergleichen

[info]    Ansichtsoptionen: Süden oben    Flache Ozeane    Setzen

Die Hufnagel-Entwürfe

Eine Präsentation der pseudozylindrischen flächentreuen Kartennetzentwürfe von Herbert Hufnagel (1989).
Hinweis: Dieser Artikel wurde am 17.11.2015 überarbeitet und erweitert. Wenn Du ihn schon zuvor gelesen hast und nun nur an den Neuigkeiten interessiert bist, springe direkt zu dem Abschnitt über die Formeln.
 

• Einleitung
• Grafiken
• Die Formeln
• Tabellarische Übersicht
• Quellen
• Annäherungen

Einleitung

Vor einiger Zeit stolperte ich im Web über Richard Capek Dokument Which is the Best Projection for the World Map? ^[2]
In diesem Dokument schlägt Capek eine Methode vor, mit der sich die Winkel- und Flächenverzerrung einer Weltkarte in einer einzigen Größe names Q darstellen lässt.

Q ist dabei der prozentuale Anteil der Karte, welcher innerhalb akzeptabler Parameter liegt – und für diese Parameter legt Capek fest, dass der maximal verzerrte Winkel 40° und die maximale Flächenverzerrung im Verhältnis 1,5 liegen darf.

Je höher der Wert, desto geringer fallen also die Verzerrungen aus: Bei 100 untersuchten Entwürfen errechnet Capek Q zwischen 84,7 (= geringste Verzerrungen) und 20,7 (= stärkste Verzerrungen).

Ich werde jetzt nicht über Capeks Dokument reden oder anmerken, dass ich es ein wenig gewagt finde, zu behaupten, man könne den besten Netzentwurf aufgrund einer Formel bestimmen (Upps! Jetzt habe ich es doch getan!) – ich halte es da eher die Carlos A. Furuti, der die Frage »Welches ist der beste aller Entwürfe?« mit einem lapidaren Das hängt vom Verwendungszweck der Karte beantwortet.

Was mich aber stutzen ließ: Innerhalb der ersten 30 Plätze von Capeks Liste waren sechs Hufnagel-Projektionen zu finden.
Hufnagel?
Nie gehört.
Also hab ich gegooglet, und siehe da: Es waren nirgendwo Abbildungen der Hufnagel-Projektionen zu finden!

Um es kurz zu machen, ich besorgte mir das Original des Artikels, in dem Herbert Hufnagel einige unecht-zylindrische Projektionen vorstellt (welcher im Fachmagazin Kartographische Nachrichten zu finden ist ^[1]) und schickte diesen Artikel an Daniel »daan« Strebe (Autor des Programms Geocart), der so freundlich war, Grafiken der Hufnagel-Entwürfe zu erstellen und sie via Wikimedia Commons zur Verfügung zu stellen.

Herzlichen Dank, daan! :-)

Hinweis: Die Grafiken von daan habe ich hier im Artikel später durch eigene ersetzt. Das war mir möglich, weil mittlerweile sowohl Geocart, als auch das freie Tool G.Projector die Hufnagel-Projektionen unterstützen.

Hier folgt also – meines Wissens zum ersten Mal im World Wide Web (abgesehen natürlich von daans o.g. Einträgen auf Wikimedia Commons) – eine Darstellung aller acht Entwürfe von Herbert Hufnagel.
Die Ordnungszahlen habe ich aus Capeks Liste übernommen, sie beziehen sich auf die Nummerierung der Abbildungen in Hufnagels Artikel – daher fehlen die Nummern 1, 5, 6 und 8: Bei den entsprechenden Abbildungen handelt es sich um die Darstellung anderer Entwürfe, die Hufnagel zu Vergleichszwecken eingefügt hat.
Alle Hufnagel-Entwürfe sind flächentreu.

 

Hufnagel leitet die Darstellung seiner Entwürfe mit folgenden Worten ein:

Der Grundgedanke für das nachstehend beschriebene System unecht-zylindrischer Kartennetze war, andere, vor allem stumpfere Meridiankurven zu erzielen, als dies die Cosinuskurven oder Ellipsen der klassischen Entwürfe sind.

(Mit den »klassischen Entwürfen« meint Hufnagel Mollweides, Eckerts und Wagners Pseudozylinder.)

Sehen wir uns also an, zu welchen Ergebnissen Hufnagel gekommen ist.

 

Grafiken der Hufnagel-Kartennetzentwürfe

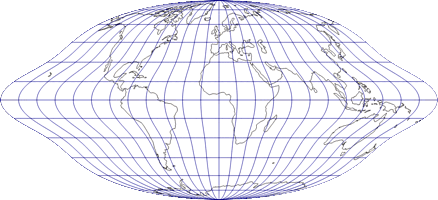
Hufnagel 2

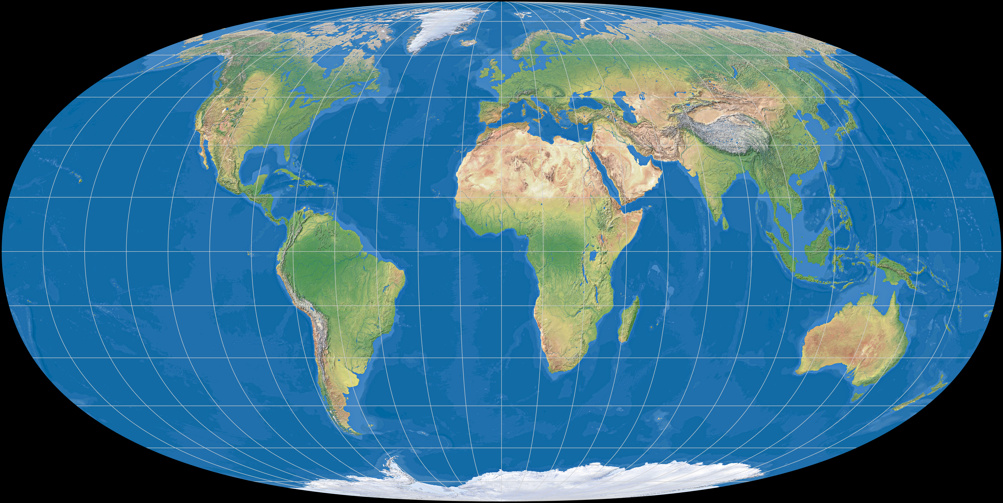
Auf den ersten Blick besitzt Hufnagel 2 eine sehr große Ähnlichkeit zu Toblers Hyperellipse – im direkten Vergleich zeigen sich die Unterschiede aber deutlicher:
Hufnagel 2 vs. Toblers Hyperellipse

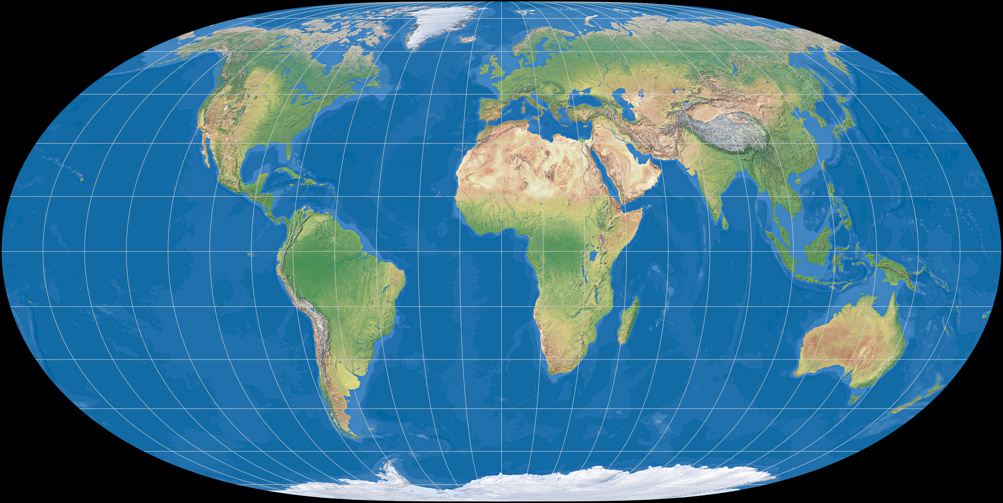
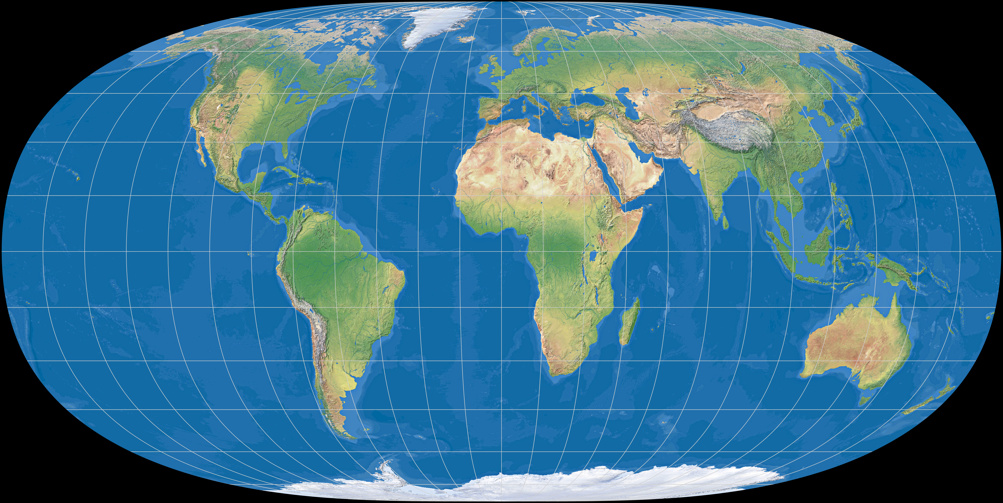
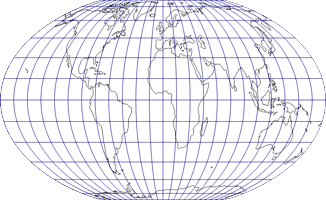
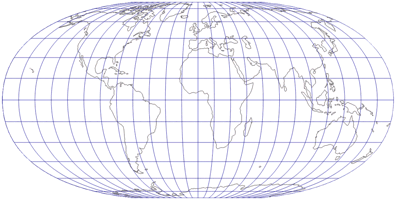
Die Entwürfe 3 und 4 sind der Nummer 2 sehr ähnlich (und bleiben daher auch nahe am Tobler), besitzen aber, so Hufnagel, »zunehmend bessere Verzerrungswerte« – was sich auch in Capeks Verzerrungswert niederschlägt: Beim Hufnagel 2 ist Q = 75,8; Hufnagel 3 kommt auf 76,7 und der vierte Entwurf wird mit 77,8 notiert.

Hufnagel 3

Hufnagel 4

Bei einer so großen Ähnlichkeit lohnen sich mal wieder die direkten Vergleiche:
Hufnagel 2 vs. Hufnagel 3
Hufnagel 3 vs. Hufnagel 4
Hufnagel 2 vs. Hufnagel 4

Übrigens merkt Hufnagel in seiner 1989er Artikel an, dass er bereits 1974 einen Netzentwurf vorgestellt hat – aus dem Zusammenhang lässt sich vermuten, dass es sich dabei um einen der drei oben genannten gehandelt haben könnte. Falls irgendjemand etwas Genaueres weiß, wäre ich für entsprechende Hinweise sehr dankbar!

 

Die folgenden drei Entwürfe weisen eine Pollinie auf – und abermals verbessern sich schrittweise die Verzerrungswerte.

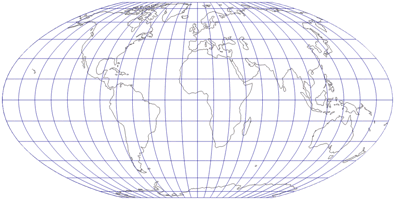
Hufnagel 7

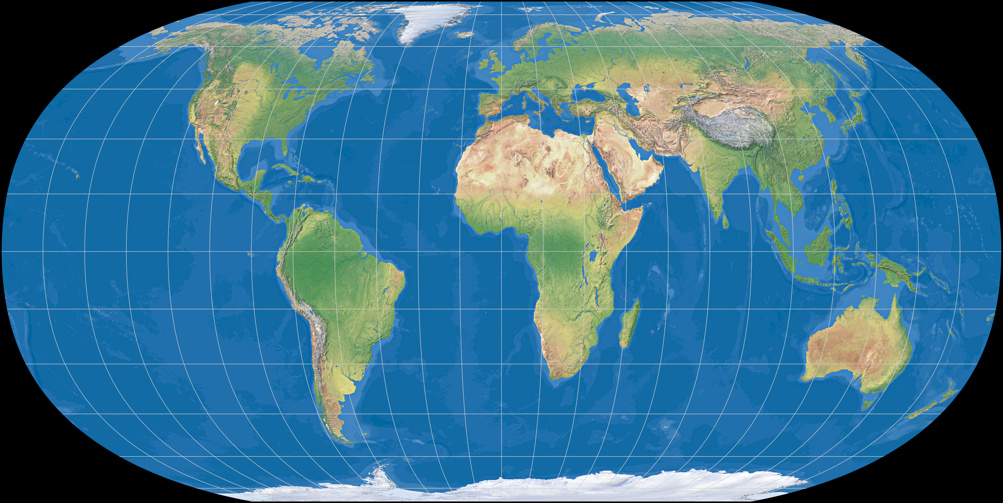
Bei Hufnagel 7 ist Q = 79,7; zudem hat er als einziger der drei keine abgerundeten, sondern spitze Ecken, was ihn zu meinem Favoriten dieser Dreier-Gruppe macht – ich scheine ein Freund spitzer Ecken zu sein. ;-)

Bei einem Blick auf Hufnagel 9 und 10 sollte jeder, der sich schon mal mit Kartennetzentwürfen beschäftigt hat, denken: »Das kommt mir doch irgendwie bekannt vor…«

Hufnagel 9

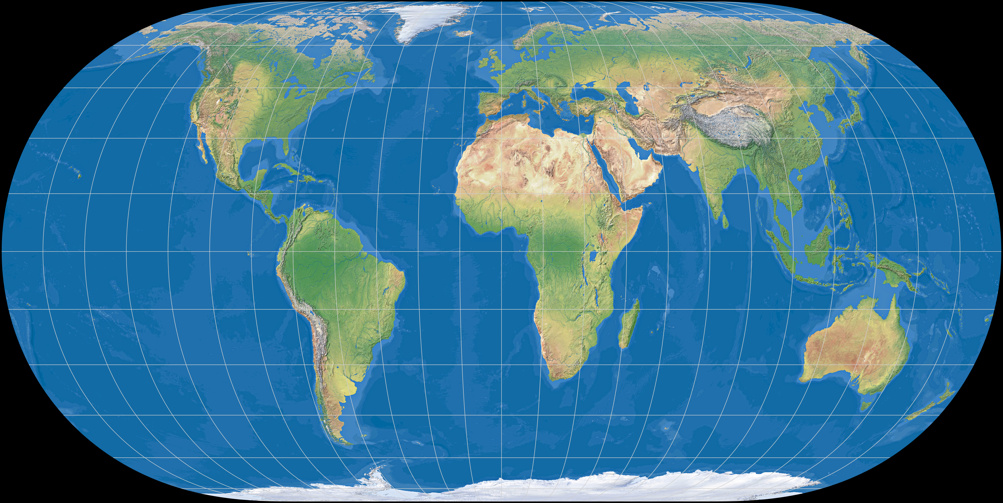
Hufnagel 10

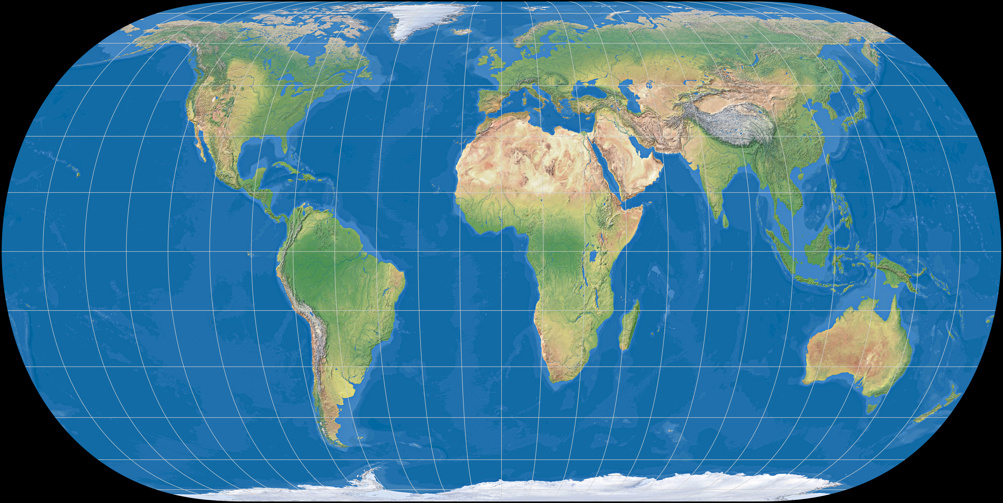
Beide sind dem altbekannten Eckert IV ähnlich, besonders aber der Hufnagel 9:
Hufnagel 9 vs. Eckert IV

Die Nummer 10 hat bessere Verzerrungswerte (Q = 83,2 gegenüber Q = 80,1 bei der Nummer 9; Hufnagel selbst beschreibt den neunten Entwurf aber als den »ästhetisch ausgewogensten« seiner Projektionen mit Pollinie. Während ich persönlich zustimmen kann, dass Hufnagel 9 etwas hübscher ist als die 10, so finde ich doch, dass Hufnagel 10 die wertvollere Ergänzung für die Welt der Kartennetzentwürfe ist:
Einerseits aufgrund der geringeren Verzerrungswerte; andererseits… nun, Hufnagel 9 ist schon sehr nahe am Eckert IV und wirkt somit eher wie eine Variation des bekannten Entwurfs, während Hufnagel 10 deutlich eigenständiger daherkommt.
Hufnagel 9 vs. Hufnagel 10

 

Mit dem nächsten Entwurf kehrt Hufnagel zu einer Darstellung mit den Polen als Punkt zurück:

Hufnagel 11

Das auffallendste Merkmal sind die Meridiane, die um die Äquator herum nicht gebogen, sondern flach sind.
Bei Capek wird der Hufnagel 11 mit Q = 78,3 gelistet und hat somit die besten Verzerrungswerte von Hufnagels Entwürfen mit Pol als Punkt. Hufnagel selbst beschreibt die Form dieses Entwurfs als »zum mindesten gewöhnungsbedürftig« – und wer bin ich schon, dass ich dem Urheber widersprechen könnte? ;-)

Nichtsdestoweniger gefällt mit der Hufnagel 11 durchaus; vor allem eben weil er sehr eigenständig wirkt.
Ganz im Gegensatz zum letzten Entwurf aus Hufnagels Reihe:

Hufnagel 12

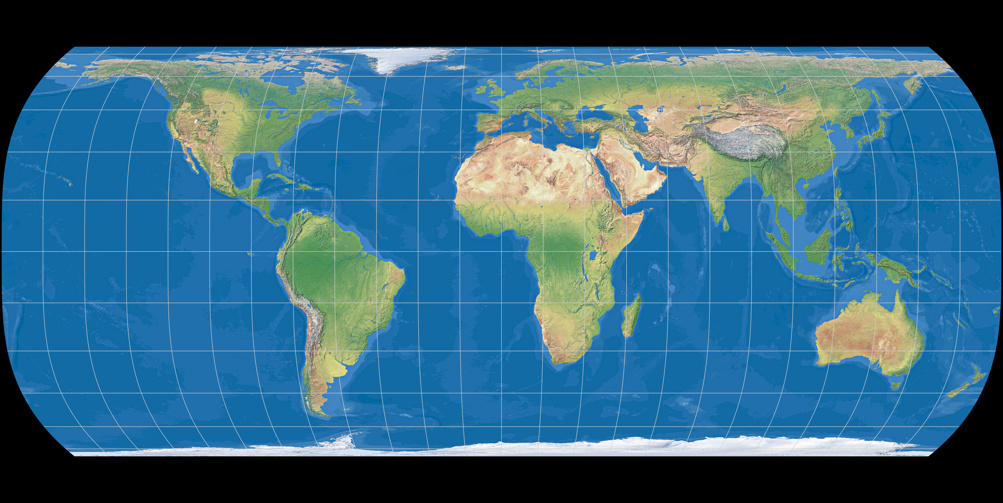
Das kennen wir doch, oder?
Hufnagel 12 ist erklärtermaßen eine Variation von Behrmanns flächentreuem Zylinderentwurf mit verringerten Verzerrungswerten (Q = 79,7 – leider nennt Capek nicht den Q von Behrmann). Und da Hufnagel selbst die Praxistauglichkeit dieses Entwurfs anzweifelt, fühle ich mich nicht genötigt, mehr darüber zu sagen.
Hufnagel 12 vs. Behrmann

 

Die Formeln

Wenn ich schon die Hufnagel-Projektionen vorstelle, sollte ich ja eigentlich auch die dazugehörigen Formeln präsentieren. Aber das überlasse ich lieber Leuten, die qualifizierter sind – die Formeln sind nachzulesen in einer Veröffentlichung von Bernhard Jenny, Bojan Šavrič und Daniel »daan« Strebe. ^[3]

Was ich aber jetzt schon zu diesem Thema sagen kann: Genau genommen, gibt es gar keine Hufnagel-Formeln (Plural), sondern eine Hufnagel-Formel (Singular): Die acht Projektionen, die Hufnagel präsentiert hat, werden dadurch generiert, dass man in dieser Formel vier bestimmte Variablen mit den entsprechenden Werten versieht. Diese Variablen hat Hufnagel A, B und Ψ_max genannt; zusätzlich lässt sich das Längenverhältnis vom Äquator zum Mittelmeridian festlegen. Als Ergebnis erhält man stets einen flächentreuen Entwurf. Und mit den richtigen Werten lassen sich dann nicht nur Hufnagels Entwürfe berechnen, sondern auch Darstellungen, die Mollweide, Eckert IV, Wagner IV und dem flächentreuen Zylinderentwurf entsprechen und Eckert VI annähern.

Aber glaubt mir nicht einfach – überzeugt Euch selbst:
Unter mapthematics.com/interactive/hufnagel.html kann man die Hufnagel-Projektionen nicht nur auswählen, sondern per Schieberegler selbst an den genannten Variablen herumdrehen. Somit kann man auf einfache Weise eigene Hufnagel-Variationen erstellen, die nützlich sein können…

… oder ein wenig an den Goode-Entwurf in seiner ununterbrochenen Form erinnern… oder Du kannst einen flächentreuen Entwurf generieren, dessen äußere From sich an den populären Winkel Tripel annähert (falls man so etwas haben möchte, was vermutlich selten der Fall ist)…

… besser gefällt mir das Resultat, wenn man dem Hufnagel 2 eine (vergleichsweise kurze) Pollinie verpasst – oder die o.g. Winkel-Tripel-förmige Variante in einem Seitenverhältnis von 2:1 erzeugt…

… oder aber man bastelt sich Projektionen, die man wohl kaum verwenden wird, aber immerhin lustig anzuschauen sind.

 
 

Natürlich sind einige der oben gezeigten Beispiele absolut überflüssig.
Aber sie zeigen doch die Flexibilität der Hufnagel-Formel – und damit auch, dass es sich um eine sinnvolle Ergänzung im Bereich der pseudozylindrischen Kartennetzentwürfe handelt.

 

Hufnagel-Projektionen – Tabellarische Übersicht

	Entwurf	Q	Dan	A	B	Ψmax	α
	Hufnagel 2	75,80	30,33	0,05556	-0,05556	90°	2
	Hufnagel 3	76,70	30,27	0,5	0,05556	90°	2
	Hufnagel 4	77,80	29,52	0,08333	-0,08333	90°	2
	Hufnagel 7	79,70	28,97	0,08333	-0,08333	60°	2
	Hufnagel 9	80,10	28,80	0,66667	-0,33333	45°	2
	Hufnagel 10	83,20	28,22	-0,66667	0,66667	30°	2
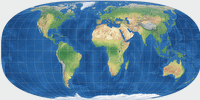
	Hufnagel 11	78,30	28,81	0	-0,11111	90°	2
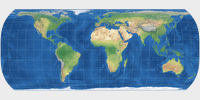
	Hufnagel 12	79,70	25,79	0	-0,11111	40°	2,44
Wie oben schon erwähnt, lassen sich einige bekannte Projektionen auch mit Hilfe der Hufnagel-Formel generieren (oder, in einem Fall, zumindest annähern). Auch für diese Entwürfe möchte ich die entsprechenden Werte nennen:
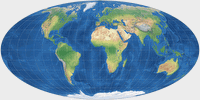
	Mollweide	70,60	32,28	0	0	90°	2
	Eckert VI (Annäherung)	69,50	32,43	-0,095	0,095	60°	2
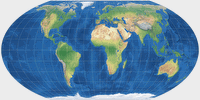
	Wagner IV	76,30	30,39	0	0	60°	2
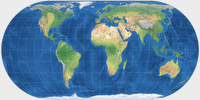
	Eckert IV	81,90	28,73	1	0	45°	2

 

Hufnagel-Annäherungen

Für eine Weile wurden hier auf der Website Annäherungen an einige der Hufnagel-Entwürfe gezeigt. Diese konnte mittlerweile ersetzt werden. Der Abschnitt über diese Annäherungen bleibt (vorerst) erhalten, siehe Approximationen.

Quellenangaben

1. ↑ Hufnagel, Herbert:
   Ein System unecht-zylindrischer Kartennetze für Erdkarten.
   In: Kartographische Nachrichten 39/3: 89-96; München Juni 1989.
2. ↑ Capek, Richard 2001:
   Which is the Best Projection for the World Map?
   icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf
3. ↑ Jenny, B., Savric, B. and Strebe, R. D. 2016
   A computational method for the Hufnagel pseudocylindric map projection family
   download at researchgate.net

Zurück zu Ausgewählte Entwürfe  •  Nach oben