Was ist eine Kartenprojektion? – Eine kurze Einführung
Die Erde ist eine Kugel.
(Nun, keine exakte Kugel, aber nah genug dran.)
Die einzige korrekte Darstellung der Erdoberfläche ist auf einem Globus zu finden.
Ein Globus zeigt die Erde, wie sie ist – aus praktischen Gründen stark verkleinert, denn die meisten
Leute haben auf ihrem Schreibtisch keinen Platz für eine Kugel mit einem Durchmesser von etwa 12.742 Kilometern.
Aber die Formen und Größenverhältnisse der Landmassen und Ozeane, ihre Lage zueinander – das alles ist korrekt.
Nun ist es aber unmöglich, die Erdoberfläche korrekt auf einer platten Karte darzustellen, was Leonhard Euler schon 1777 mathematisch bewiesen hat. Ein übliches Alltagsbeispiel ist es, sich vorzustellen, man wollte die abgepellte Schale einer Orange flach auf einen Tisch legen: Die Schale wird sich an einigen Stellen wölben und an anderen einreißen.
Da das also nicht funktioniert, behilft man sich mit einer Projektion:
Man stelle sich vor, die Erde sei durchscheinend, man habe eine Lichtquelle und ein großes (richtig großes!)
Stück Papier, welches man um die Erde wickelt und das als Leinwand fungiert, auf die das Bild geworfen wird.
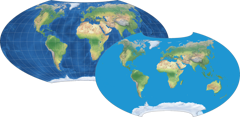
Die schematische Darstellung zeigt diese Anordnung.
Das sollte klarmachen, wie man sich das vorstellen muss – und warum man von Kartenprojektionen spricht.
Und wenn man sich mal Grönland anschaut (die violette Insel ganz oben auf dem Globus and der Karte), sieht
man auch sofort die Verzerrungen, zu denen dieses Verfahren führt.
Aber die Darstellung zeigt nur eine mögliche Art, die Projektion einzufangen.
Abhängig davon, wo man die Lichtquelle platziert, wie man das Papier um die Erde wickelt
– sofern man es überhaupt rumwickelt und nicht flach neben die Erde legt –,
an welcher Stelle das Papier die Erde berührt (wenn überhaupt) usw., wird ein ganz anderes Bild
auf die Leinwand geworfen. Bei diesem Bild wird dann z.B. nicht Grönland verzerrt, sondern vielleicht Afrika.
Und am wichtigsten: Die meisten Kartennetzentwürfe funktionieren nicht einmal auf diese Weise!
Man könnte sie mit Hilfe einer optischen Projektion nicht herstellen; stattdessen bannen sie die kugelförmige Erdoberfläche
aufgrund von rein mathematischen Formeln auf die platte Karte. Kartographen sprechen daher in solchen Fällen
auch nicht von einer »Kartenprojektion«, sondern eben vom (Karten-) Netzentwurf oder von der Kartenabbildung.
Auf dieser Website aber werden die Begriffe als Synonyme verwendet: Ich sage auch dann »Kartenprojektion«, wenn es sich
nach kartographischer Fachterminologie um keine Projektion handelt! (Die Gründe dafür habe ich in
Eigentlich heißt es Kartennetzentwurf ausführlich dargestellt.)
Man hat also die unterschiedlichsten Möglichkeiten, die Erdoberfläche auf eine platte Karte zu bannen, aber eins bleibt immer gleich:
Man kann die Erde nicht genau darstellen, also versucht man sie annäherungsweise darzustellen.
Dazu ist man gezwungen, manche Teile der Erdoberfläche zu strecken, andere zu stauchen, vielleicht zu biegen. Das führt zu Verzerrungen.
Es ist wichtig, sich zu vergegenwärtigen, dass jede Weltkarte irgendeine Form von Verrzerrung aufweist!
Aber man kann unterschiedliche Stellen der Erde verzerren, man kann unterschiedliche Arten der Verzerrung wählen. Eine spezifische Kombination dieser Möglichkeiten nennt man Projektion. Und es gibt hunderte von verschiedenen Projektionen, jede von ihnen mit ihrer ganz eigenen Art und Verortung der Verzerrungen, in vielen verschiedenen Formen.
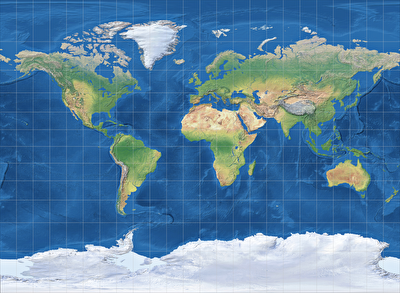
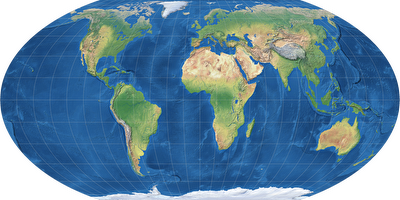
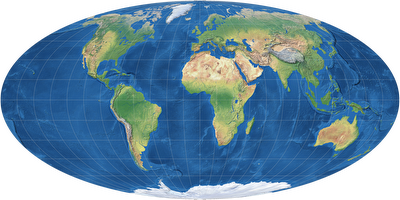
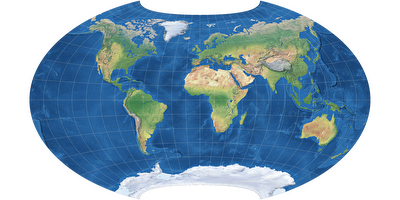
Von links nach rechts und oben nach unten: Miller, Wagner IV, Mollweide, Canters W14.
Und keine dieser unterschiedlichen Projektionen ist wirklich genau, keine ist falsch, keine ist an sich besser oder schlechter als die anderen. Sie sind unterschiedlich, sie dienen unterschiedlichen Zwecken, sie wollen unterschiedliche Aspekte hervorheben.
Man kann sagen, dass man für einen bestimmte Darstellung eine falsche Projektion gewählt hat – aber eben nur die falsche für diesen bestimmten Zweck; in anderen Situationen mag die »falsche« Projektion wiederum genau die richtige sein.
Zurück zu Grundwissen • Nach oben
Kommentare
3 Kommentare
Es gibt weitere Kommentare in der englischen Version.
Wolfram Hüttermann
Georg Steidl
man malt den Globus mit "Gnitsch"-Farbe an, und lässt ihn dann über eine 2D-Papierfläche abrollern/abfärben
Gibt's das schon ? Wie schaut das aus?
Tobias Jung
Georg Steidl
Ja doch, mathematisch ist das ja 1:1, man rollt nach oben und unten, links und rechts -> Kreis (auf der 2D-Karte),
Beispiel: man legt plan einen Ring auf den Globus (geht für "Mittelsenkrechten"), rollt ihn dann auf Karte ab ->ergiebt gleiche Länge. das geht dann für jede beliebiges Strecken-(Ring)segment auf der 3D-Oberfläche bzw. jeder Linie in 2D. Wenn alle (Quer-)Strecken -> Flächen z.B. von Afrika gezeichnet wurden, müsste sich eigentlich ach eine winkeltreue Zeichnung ergeben
das ist nicht die 'Flucht'-perspektivische (2D-)Sicht auf einen Globus, we man es gewohnt ist, könnte eher der direkten (Lineal- etc.)Messung für Seekarten dienen oder direktem Größenvergleich Länder.
ich find unter den 'azimuthalen' aber nix was das wirklich widerspiegelt
youtu.be/ZLb8tc7wJ08?t=2207
Vlt ruf ich Sie mal an
Tobias Jung
Vielleicht verstehe ich das jetzt falsch, aber eigentlich klingt mir das sehr nach dem Konstruktionsprinzip der American Polyconic Projektion, die aber dann doch ganz anders aussieht, als man das vielleicht erwartet:
https://kartenprojektionen.de/…
Ich finde jetzt gerade leider kein deutschsprachiges Dokument, in dem die Konstruktion beschrieben ist, aber in der engl. Wikipedia wird darauf eingegangen:
https://en.wikipedia.org/wiki/…
Und hier kann man mittels Schieberegler die Anzahl der »Papierstreifen« oder »-ringe« einstellen, was dabei hilft zu verstehen, warum bei diesem Vorgehen am Ende eine Projektion wie die American Polyconic herauskommt:
https://www.jasondavies.com/ma…
Sollte ich das Konstruktionsprinzip Ihrer Idee missverstanden haben, wäre u.U. eine Visualisierung, also z.B. eine Zeichnung, vermutlich sehr hilfreich.
anna
Tobias Jung
Außerdem lösche ich ja keine Kommentare, sondern Trollpostings.


Georg Steidl
Welche der Varianten entspricht denn der Lagrangeprojektion ?
Finde Canters W14 kommt am natürlichstem rüber, wie ein Torus