»Passend skaliert« vs. »auf gleiche Breite skaliert«
oder: Wie vergleicht man Netzentwürfe miteinander?
Bei dem Vergleich der Kartenprojektionen sieht man (im Experten-Modus), dass die
Grafiken einmal »passend skaliert« und einmal »auf gleiche Breite skaliert« sind.
Was soll das eigentlich heißen?
Warum ist das sinnvoll?
Die kurze Antwort
Kartennetzentwürfe haben unterschiedliche Seitenverhältnisse, was man an den hier gezeigten, kleinen Bildern
ja gut sehen kann: Die Seitenverhältnisse reichen von 1:1 bei der Lambertschen Azimuthalprojektion bis hin
zu etwa 3,13:1 bei Lamberts zylindrischem Entwurf.
Wenn man sie nun miteinander vergleichen will, muss man einen Weg finden, dass diese unterschiedlichen Größen
irgendeinen Bezug zueinander haben.
»Auf gleiche Breite skaliert« ist ja einfach zu verstehen: In diesem Fall sind die
Projektions-Grafiken immer gleich breit (und zwar etwa 1000 Pixel).
Aber was ist dieses »passend skaliert«?
Das heißt, sie wurden so skaliert, dass sie optimal in eine Fläche mit dem Seitenverhältnis
2:1 passen – auch das kann man bei den Bildern rechts schön sehen, die ich hier in einen solchen
Rahmen gepackt habe. In vielen Fällen läuft das darauf hinaus, dass beide Projektionen
die gleiche Höhe haben.
Bei manchen Paarungen ist es sinnvoller, sie »passend skaliert« zu vergleichen – bei anderen wiederum ist es sinnvoller, sie »auf gleiche Breite skaliert« zu vergleichen. Darum habe ich einfach beide Möglichkeiten eingebaut.
Und wie kam ich überhaupt auf die Idee, die Projektionen ausgerechnet in einem Rahmen im Seitenverhältnis 2:1 zu packen? Nun, das ist ganz einfach: Die Software, die ich zuerst zum Erstellen der Grafiken benutzte, macht das ganz automatisch so. Sie exportiert immer Grafiken mit diesem Seitenverhältnis, mit der eigentlichen Projektion horizontal und vertikal zentriert, und einer Hintergrundfarbe, die den Rest der Grafik auffüllt, bis dieses Seitenverhältnis erreicht ist.
Später habe ich dann zwar angefangen, auch andere Programme zu nutzen, welche diesbezüglich anders funktionieren; aber zu diesem Zeitpunkt hatte ich natürlich schon eine Dutzende von Bildern mit im 2:1-Seitenverhältnis, also habe ich es einfach beibehalten.
Das war also die kurze Antwort.
Wenn die für Dich ausreichend war, kannst Du an dieser Stelle aufhören zu lesen.
Andernfalls gehen wir nun zur lange Antwort über…
Die lange Antwort
Wer sich schon ein bisschen mit Karten beschäftigt hat, wird schnell auf die Idee kommen, dass es doch das beste sei, die beiden Projektionen, die man vergleichen will, im gleichen Maßstab darzustellen, also etwa 1:90 000 000 oder so, wie man das von Atlanten kennt.
Es gibt mehrere Gründe, warum ich mich dagegen entschieden habe.
Zunächst einmal bietet die o.g. zuerst benutzte Software die Option, Karten in einem bestimmten Maßstab zu exportieren, gar nicht an.
Ich kann die Größe der Grafik in Pixeln angeben, aber das ist auch alles.
Zweitens habe ich schon bei der Erklärung der Eigenschaft »längentreu«
darauf hingewiesen, dass der Maßstab einer Karte ein eher nomineller Wert ist, der aber nur
auf einigen wenigen Strecken der Karte tatsächlich zutreffend ist. Und das gilt für gedruckte Karten,
die ja immer gleich groß sind!
Auf einer Webseite kommt ein weiteres Problem hinzu:
Die Grafiken hier haben eine Breite von etwa 1000 Pixeln.
Wenn ich einen Zollstock an meinen Monitor halte, sehe ich, dass das etwa 26,5cm sind. Aber auf anderen
Monitoren kann dabei ein anderer Wert herauskommen, das hängt nämlich von der Bildschirmdiagonalen und der Auflösung des Monitors
ab. Und dann gibt es ja nicht nur Monitore!
Auf unserem Tablet sind die Grafiken zwischen 13,5cm und 20cm breit; abhängig davon, ob ich das Ding im Hoch- oder Querformat
halte und ob ich gezoomt habe oder nicht.
Für Grafiken im Web wäre eine Maßstabsangabe also Firlefanz.
Und als ich anfing, an dieser Website zu arbeiten, war ich mit den erzeugten »passend skalierten« Grafiken auch zufrieden.
Aber dann bin ich über einen bestimmten Vergleich gestolpert – nämlich Ginzburg V vs. Ginzburg VI. Beim passend skalierten Vergleich
sehen diese beiden so aus:
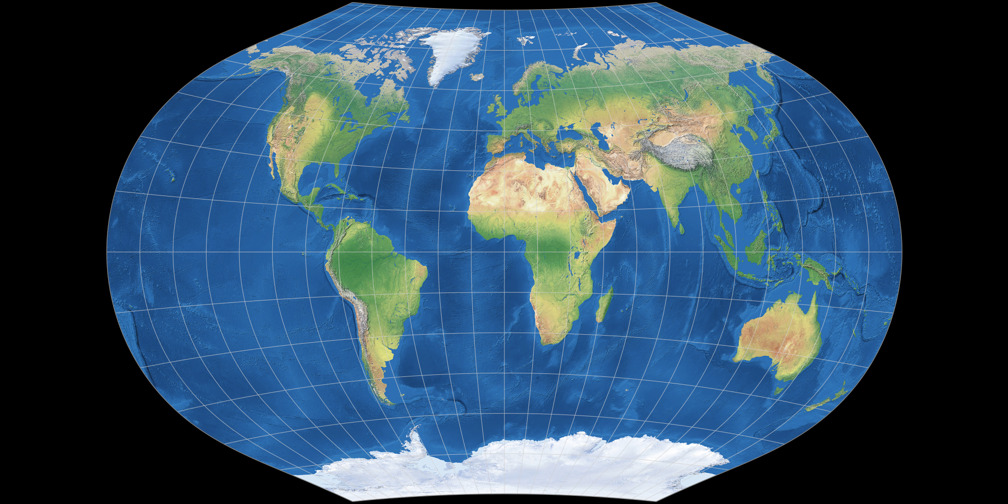
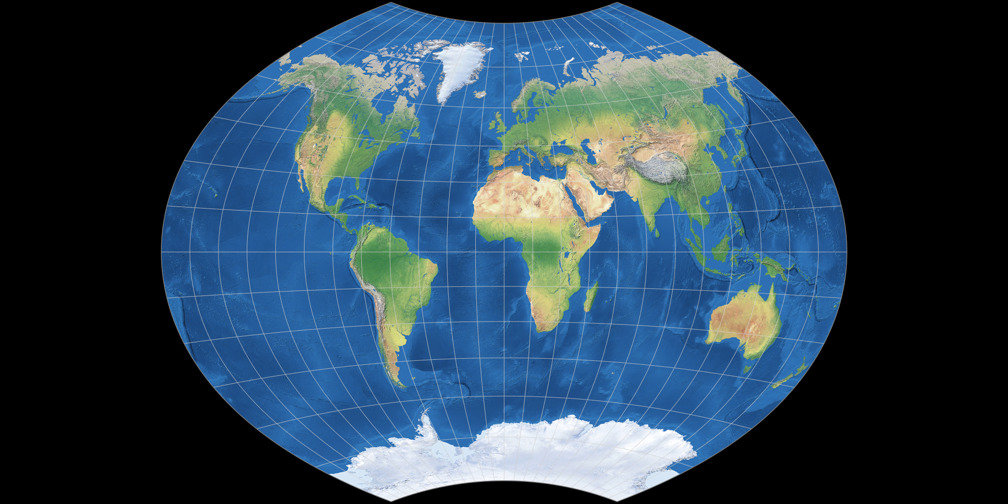
Wie man sieht: Gleiche Höhe der Projektionen, aber sie sind unterschiedlich breit.
Dabei habe ich mir auch die ganze Zeit nichts gedacht, bis mir irgendwann die Idee kam, man könne
sie mit Hilfe eines Grafikprogramms auch so anpassen, dass sie die gleiche Breite haben.
Das sah dann so aus:


In der Mitte – grob gesagt zwischen 45° Nord/Süd und 75° Ost/West – sind beide Karten fast identisch!
Und ich vermute, dass ist genau das, was Herr Ginzburg beabsichtigt hatte, als er seine Projektionen entwarf.
Andererseits haben wir den Wagner IX.
In seinem Buch Kartographische Netzentwürfe stellte Wagner zwei Varianten dieses Entwurfs vor:
Zunächst einmal präsentierte er die Formel. Und dann fügte er eine Abbildung hinzu, die von dieser Formel abwich:
Nun kann man (…) eine weitere Verbesserung in der Verteilung der Verzerrungen erzielen, wenn man das ganze Netz in Richtung des Äquators noch ein wenig zusammendrückt. Zu diesem Zweck versieht man die x noch mit einem Faktor a < 1 (…) Die Abbildung weist eine Zusammendrückung in Richtung des Äquators auf, und zwar ist a = 0,88 gewählt.
In diesem Falle scheint die Skalierung auf gleiche Breite also weniger angebracht zu sein, sondern es ist besser,
sie in der passend skalierten Version zu betrachten.
Hinweis: Hier auf kartenprojektionen.de wird der Entwurf nach Wagners Formel
als Wagner IX bezeichnet, jener nach Wagners Abbildung als Wagner IX.i.
Wagner IX vs. Wagner IX.i
Also habe ich mich gefragt: Welchen Vergleich sollte ich nehmen, wenn einmal der eine und einmal der andere angemessener erscheint?
Da gab es nur eine Antwort: Beide.
Dadurch wurde der Vergleich aber ein bisschen unübersichtlich, und ich habe ihn in den Einfachen und den Experten-Modus unterteilt: Den einfachen Modus für alle, die nur einen kurzen Blick auf den Vergleich werfen wollen; und den Experten-Modus für eine genauere Analyse der Unterschiede.
Kommentare
Sei der erste, der einen Kommentar hinterlässt!