Die metrischen Eigenschaften von Kartennetzentwürfen
(wie sie hier benutzt werden)
Hätte ich diesen Artikel früher gekannt, hätte ich ihn vielleicht einfach übernommen und übersetzt…
Neben den unterschiedlichen Gruppen von Kartenprojektionen gibt es unterschiedliche Abbildungs- oder auch
Verzerrungseigenschaften, nach denen man sie klassifizieren kann.
In meinen Augen ist die Kenntnis der unterschiedlichen Eigenschaften sogar noch wichtiger – zumindest für den alltäglichen
Gebrauch von Weltkarten.
Auf dieser Website habe ich die Projektion in vier Eigenschafts-Kategorien eingeteilt, die ich im folgenden kurz erkläre.
Winkeltreue (konforme) Projektionen
Bei der winkeltreuen oder konformen Darstellung entsprechen alle Winkel auf der Karte örtlich den Winkeln in der realen Welt.
Daher folgen zwei beliebige Linien in der Karte dem gleichen Winkel wie die entsprechenden Ursprungslinien auf der Erde;
insbesondere kreuzen sich projizierte Gradnetzlinien immer im rechten Winkel.
In der Seefahrt wurde über Jahrhunderte nur eine bestimmte winkeltreue Karte, die Mercator-Projektion benutzt:
Auf dieser entspricht ein gerader Kurs auf See einer geraden Linien auf der Karte.
Während winkeltreue Karten also für die Navigation unerlässlich sind, haben sie für die meisten anderen Zwecke einen gewaltigen Nachteil:
Sie verzerren die Größenverhältnisse, und zwar gewaltig! Vielleicht denkst Du, dass die unten abgebildete Mercator-Projektion – die
eindeutig bekannteste konforme Darstellung – die Größenverhältnisse korrekt darstellt.
Vielleicht auch nicht, weil Du Dich schon mit Weltkarten beschäftigt hast, oder eine ganz bestimmte Folge der Serie
The West Wing – Im Zentrum der Macht gesehen hast. ;-)

Die Mercator-Projektion mit ihren erheblichen Größenverzerrungen
Auf jeden Fall ist die Mercator-Projektion so weit verbreitet, dass viele Leute tatsächlich annehmen, sie sei diesbezüglich korrekt. Aber während auf dieser Karte Grönland etwa genauso groß wie Afrika zu sein scheint, ist Afrika (30.221.532 km²) in Wirklichkeit fast vierzehnmal größer als Grönland (2.166.086 km²).
Zur Verdeutlichung schauen wir uns die stereographische Projektion an, die ebenfalls zu den winkeltreuen gehört:
Es würde wohl niemand vermuten,
dass es sich hierbei um eine korrekte Darstellung der Welt handelt. Nichtsdestoweniger hat sie ganz ähnliche Verzerrungen
der Größenverhältnisse wie die Mercator-Projektion. Sie ist also genauso richtig – oder genauso falsch – wie der Mercator.
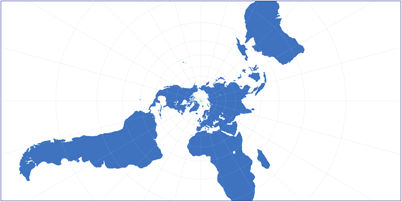
Stereographische Projektion, polständig
Es wird oft gesagt, dass winkeltreue Netzentwürfe die Formen auf der Erde nicht verzerren. Das stimmt allerdings nur lokal – auf einer Weltkarte hingegen kommt die Größenverzerrung irgendwann der Formtreue in die Quere. Bei der stereographischen Projektion lässt sich der sehr gut am Beispiel von Südamerika beobachten: Würde man den Kontinent in viele kleine Quadrate zerschneiden, würde jedes dieser Quadrate den jeweligen Ausschnitt sehr formgerecht darstellen. Aber dadurch, dass die Südspitze deutlich stärker vergrößert wird als die nördlichen Bereiche, wird die Gesamt-Form des Kontinents ebenfalls verzerrt.
Flächentreue (äquivalente) Projektionen
Die Erklärung von flächentreuen Projektionen ist ganz einfach:
Sie stellen die Erde mit korrekten Größenverhältnissen dar.
Wie gesagt, ist Afrika in der Realität vierzehnmal größer als Grönland – und genauso verhält es sich auf einer
flächentreuen Karte. So einfach ist das. :-)
Für die Flächentreue muss die Karte aber einen Preis zahlen:
Die Formen werden verzerrt. Und das fast überall auf der Karte. Normalerweise wird ein kleiner
(ein sehr kleiner) Bereich auf der Karte ohne Formverzerrung dargestellt; aber je weiter man sich von
diesem Bereich entfernt, desto stärker fallen die Verzerrungen aus.
Übrigens hat man flächentreue Entwürfe früher oft auch als äquivalente Projektionen bezeichnet.
Dieser Begriff wird im Deutschen kaum noch verwendet, im englischen Sprachraum trifft man aber noch häufig den
entsprechenden Ausdruck equivalent map.
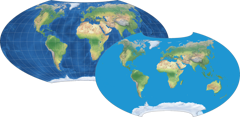
Und damit ist genug gesagt. Schauen wir uns noch zwei Beispiele für flächentreue Netzentwürfe an und kommen dann zur nächsten Kategorie.
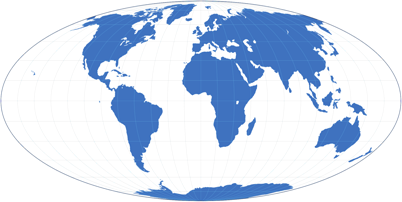
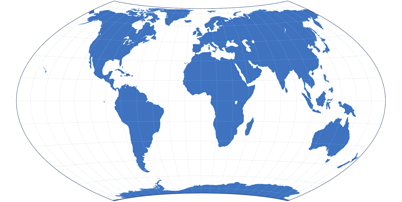
Zwei flächentreue Projektionen: Mollweide (links) und Wagner VII
Vermittelnde (aphylaktische) Projektionen
Wir rekapitulieren:
Winkeltreue Projektionen bewahren die Formen sehr gut, verzerren aber die Größenverhältnisse.
Flächentreue Projektionen zeigen die Größenverhältnisse korrekt, verzerren aber die Formen erheblich.
Was liegt also näher, als einen Kompromiss zu entwerfen?
Entwürfe, die sowohl die Formen, als auch die Größenverhältnisse verzerren – beides aber in
geringerem Ausmaß. Und genau das tun die vermittelnden Projektionen.
Anmerkung 28.8.2015:
Ich habe gerade erst herausgefunden, dass vermittelnde Entwürfe gelegentlich auch
aphylaktisch genannt werden.
Mir gefällt dieser Begriff sehr gut, deshalb nehme ich mir vor, ihn in Zukunft gelegentlich
zu benutzen. :-)
Sie versuchen, die Verzerrungen von Größe und Form auszubalancieren; folglich sind sie an keinen Punkt der Karte »genau« (im Sinne des korrekten Übertragens von metrischen Eigenschaften), aber möglicherweise vermitteln sie genau dadurch sogar ein besseres Bild der Erde als die beiden oben genannten Arten.
Ein sehr gutes Beispiel für vermittelnde Entwürfe ist die Robinson-Projektion, da es das erklärte Ziel ihres Urhebers Arthur H. Robinson war, eine Weltkarte zu erschaffen, die korrekt wirkt und ein gefälliges Gesamtbild vermittelt, anstatt die Erdoberfläche anhand von mathematischen Formeln auf eine flache Karte zu projizieren.
Und also ging er auch nicht mathematisch vor: Vereinfacht gesagt, zerrte er so lange an den Formen und Größen herum, bis er der Meinung
war, dass das Ergebnis gut aussieht, und kümmert sich danach um die mathematische Umsetzung der Projektion.
Daher kann die Robinson-Projektion auch nicht mit einer Formel beschrieben werden, stattdessen basiert sie auf einer Tabelle von
Breitengeraden und ihren Verzerrungswerten.
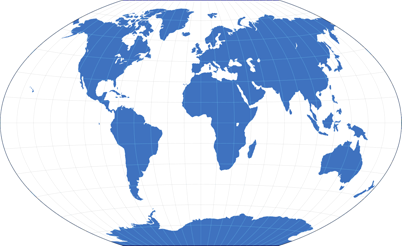
Und das Ergebnis kann man meiner Meinung nach durchaus als gelungen bezeichnen.
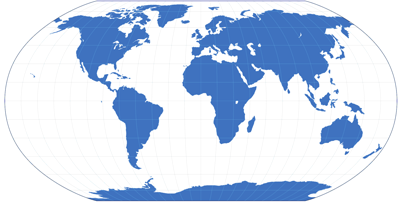
Die vermittelnde Robinson Projektion
Die Robinson-Projektion diente der US-amerikanischen National Geographic Society (NGS) von 1988 bis 1998 als Referenzkarte und wurde dann ersetzt durch Winkel Tripel – eine weiterer vermittelnder Entwurf. Falls Du, wie ich, in den 1970er Jahren (oder später) in die Schule gegangen bist, ist Dir diese Projektion vielleicht aus dem weitverbreiteten Diercke Weltatlas bekannt.
Längentreue (äquidistante) Projektionen
Die längentreuen Projektionen habe ich an das Ende dieses Artikels gesetzt, weil ihre Erklärung ein wenig längert dauert – und auch, weil ich persönlich der Meinung bin, dass diese Eigenschaft am uninteressantesten ist.
Aber ich fange mit einer kurzen Variante der Erklärung an:
Längentreue Projektionen lassen eine maßstabsgerechte Messung der Entfernung an gewissen Linien zu.
Verstanden?
Nein?
Dann geht es Dir wie mir.
Doch? Dann bist Du schlauer als ich und brauchst den Rest des Artikel nicht mehr zu lesen…
Also, hier kommt die lange Version der Erklärung:
Hast Du jemals versucht, die Entfernung zwischen zwei Punkten auf der Erde – sagen wir mal, die Luftliniendistanz
zwischen Rom und New York – anhand einer gedruckten Welkarte zu ermitteln, indem Du ein Lineal an die Karte gehalten,
die Distanz in Zentimetern gemessen und diesen Wert mit dem auf der Karte angegebenen Maßstab multipliziert hast?
Nun, Du hast nicht das richtige Ergebnis bekommen.
Zum Beispiel:
Ich habe eine Weltkarte (Wagner-VIII-Projektion) im Maßstab 1 : 75.000.000.
Von Rom nach New York messe ich 10,6 cm; umgerechnet ergibt das eine Entfernung von etwa 7.950 km.
Schaue ich aber im Web nach, so wird mir gesagt, dass die Entfernung zwischen Rom und New York ca. 6.889 km beträgt.
Also, was ist da falsch gelaufen? Hab ich mich verrechnet? Haben die Hersteller der Karte einen Fehler gemacht?
Nein, nichts davon.
Die Sache ist die: So funktioniert das einfach nicht.
Wie ich an anderer Stelle schon ausgeführt habe, weist jede Weltkarte irgendeine Art von Verzerrung auf. Diese Verzerrungen sind es, die zum falschen Ergebnis führen.
Da es sich beim Wagner VIII um eine vermittelnde Projektion handelt: Habe ich vielleicht nur den falschen Kartentyp für meine Messung herangezogen? Hätte ich eine längentreue Karte nehmen sollen? – Nein, auch da wäre ich zu einem falschen Ergebnis gekommen; jedenfalls in den allermeisten Fällen.
Und das liegt daran, dass der Begriff längentreu falsche Vorstellung erwecken mag: Man könnte denken,
dass auf einer solchen Karten alle Entfernungen maßstabsgetreu wiedergegeben werden – allerdings werden
auf jeder längentreuen Karte nur bestimmte Entfernungen maßstabsgetreu gezeigt.
Auf der quadratischen Plattkarte gilt dies für Entfernungen entlang der Längengerade. Man kann diese Karte also
verwenden, um beispielsweise die Entfernung zwischen Hamburg und Duala, der größten Stadt Kameruns, zu messen – beiden
liegen etwa auf 10° Ost.
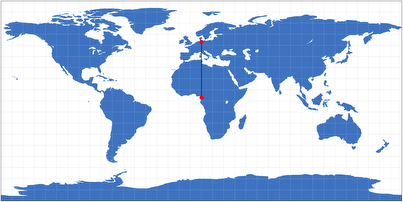
Quadratischen Plattkarte mit der Entfernung Hamburg - Duala
Aber für die meisten Strecken braucht man eine spezielle Karte. Um auf das Beispiel Rom – New York zurückzukommen: Hier bietet sich die mittabstandstreue Azimutalprojektion an. Auf dieser Karte sind die Entfernungen jedes Punktes zum Kartenmittelpunkt korrekt wiedergegeben. Sehen wir uns eine Karte an, bei der New York in den Mittelpunkt gerückt wurde:
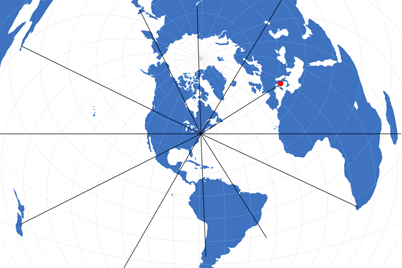
Mittabstandstreue Azimutalprojektion mit New York im Mittelpunkt
Entlang der schwarzen Linien (und allen anderen, nicht eingezeichneten, die zum Mittelpunkt führen) lassen sich die Entfernungen maßstabsgetreu messen – unter anderem eben auch zu Rom (roter Punkt). Und wenn Du nun die Entfernung zwischem Rom und Rio de Janeiro messen willst? – Dann brauchst Du eine andere Karte.
Ein letztes Beispiel: Die Two-Point-Equidistant Projection.
Ich habe keine »offizielle« Übersetzung der Bezeichnung gefunden – vermutlich würde sie so ähnlich wie
Längentreue Projektion mit zwei Kontrollpunkten lauten…
Es handelt sich dabei sozusagen um eine erweiterte Variante der mittabstandstreuen Azimutalprojektion,
denn hier werden zwei Punkte festgelegt (die vom Urheber der Karte beliebig ausgewählt werden können); die
Entfernungen von diesen beiden Punkten zu jedem anderen Punkt auf der Karte – und somit natürlich auch
vom ersten zum zweiten Kontrollpunkt – sind maßstabsgerecht wiedergegeben.
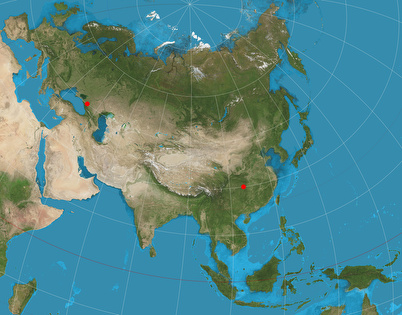
In dieser Grafik wurden die Kontrollpunkte auf 45° Nord, 40° Ost und 30° Nord, 110° Ost gelegt:
Aber abermals gilt: Für alle anderen Punkte kann man keine maßstabsgetreue Messung der Entfernung vornehmen, dafür müsste man die Karte in einer anderen Konfiguration neu erzeugen. Immerhin ergibt die hier gezeigte Konfiguration eine ansprechende und relativ verzerrungsarme Karte von Eurasien – das ist ja auch schon etwas wert!
Abschließend möchte ich noch darauf hinweisen, dass eine Projektion sowohl flächen-, als auch längentreu sein kann, z.B.
ist die Sinusoidal-Projektion längentreu entlang der Breitenkreise, Stab-Werner stellt die Breitenkreise, den Zentralmeridian
und sämtliche Entfernungen vom Nordpol längentreu dar – aber beide sind auch flächentreu.
Die Frage, ob eine vermittelnde Projektion auch längentreu sein kann, hängt von der Definition des Begriffs vermittelnd ab:
Definiert man diesen Begriff als Abwesenheit jeder anderen festgelegten Eigenschaft, dann kann eine Projektion
selbstverständlich nicht gleichzeitig vermittelnd und längentreu sein. Andererseits: Definiert man vermittelnd als
Mittelweg zwischen Äquivalenz und Konformität – ja, dann kann ein Entwurf sowohl vermittelnd, als auch längentreu sein.
Ich bevorzuge die letztgenannte Definition.
Darum habe ich z.B. Wagner VI als vermittelnde Projektionen eingeordnet, obwohl sie den Äquator und den Zentralmeridian
längentreu abbildet. In der Gruppe der Längentreuen habe ich nur jene Projektionen belassen, deren Haupt-Eigenschaft
(in meinen Augen) darin liegt, bestimmte Strecken längentreu darzustellen.
Kommen wir noch zu einer Eigenheit der deutschen Sprache:
Manche Projektionen – etwa Eckert III und Wagner VI – haben gleichabständige Breitenkreise. Diese werden abstandstreu oder
abweitungstreu genannt. Gelegentlich werden diese Begriffe mit Längentreue gleichgesetzt. Dies ist meiner Ansicht
nach aber nicht richtig. Die rechteckige Plattkarte z.B. ist zwar sowohl längen-, als auch abweitungstreu.
Beim Wagner VI hingegen haben die Breitenkreise zwar den gleichen Abstand zueinander – aber lediglich der Mittelmeridian ist
längentreu.
Innerhalb dieser Website verwende ich den Begriff der Längentreue bzw. Äquidistanz also nur im Sinne der o.g. langen Definition;
bei gleichabständigen Breitenkreisen spreche ich von »abweitungstreu« (da mir bei dem Begriff »abstandstreu« die Verwechslungsgefahr
zu »längentreu« höher erscheint).
Zurück zu Grundwissen • Nach oben
Kommentare
Ein Kommentar
Es gibt weitere Kommentare in der englischen Version.
SF
Erstmal Kompliment für die Seite, wir haben das Thema gerade im Studium und ich finde es von Null auf recht kompliziert da direkt durchzusteigen. Diese Seite hilft da schon enorm weiter. Hätte aber mal eine Frage.
Unser Prof hat uns folgende Klassifizierungsmöglichkeiten genannt um einen Netzentwurf einzuordnen:
1. Projektionszentrum: gnomonisch, stereographisch, orthographisch
2. Abbildungsfläche: Azimutalprojektion, Zylinderprojektion, Kegelprojektion
3. Ausrichtung Abbildungsfläche: polständig, äquatorständig, zwischenständig
4. Verzerrungseigenschaften: winkel, flächen, längentreu (mittabstands, abweitungstreu)
Er erwartet dass wir die Abbildung einer Karte genau charakterisieren können, also Karte XY ist eine polständige, längentreue stereographische Azimutalprojektion als Bsp. (falls so eine Abbildung überhaupt möglich ist).
Ich weiß was die einzelnen Begriffe bedeuten, aber mir fällt es allerdings total schwer aus einem Kartenausschnitt zu erkennen um was für einen Entwurf es sich handelt. Gibt es da Aspekte an denen man sich orientieren kann ?
Falls ich eine Projektion der gesamten Kugel habe z.B. in Form des Zylinders kann ich da ja zumindest an der rechteckigen Kartenform erkennen, dass es sich um einen Zylinder handeln muss. Habe ich allerdings nur einen Ausschnitt dieser Karte, z.B. nur Afrika könnte ich nicht erkennen worum es sich handelt und schon gar nicht ob Afrika dort jetzt längen-, flächen-, oder längentreu ist.
Ich hoffe ich habe mein Problem halbwegs verständlich geschildert und es gibt jemanden der mir weiterhelfen kann.
Danke!
Tobias Jung
erstmal vielen Dank für das Kompliment! :-)
Was Deine Frage angeht: Puuuh, meiner Meinung nach stellt Euer Prof aber wirklich verdammt hohe Ansprüche! Ich muss sagen: Ich selbst könnte das nicht – zumindest nicht bei jeden beliebigen Kartenausschnitt! Ich habe mal auf die schnelle drei kleine Beispiele mit dem Programm G.Projector angelegt (ich habe in den Grafiken unten links jeweils einkopiert, welche Projektion mit welchen Parametern ich gewählt habe).
Erstens, den flächentreuen Azimutalentwurf:
http://kartenprojektionen.de/i…
Zweitens, Lamberts winkeltreue Kegelprojektion:
http://kartenprojektionen.de/i…
Und drittens, Albers flächentreue Kegelprojektion:
http://kartenprojektionen.de/i…
Natürlich sind die nicht zu 100% identisch; aber ich könnte auf keinen Fall bestimmen, welche Grafik nun in welcher Projektion vorliegt.
Und genau so hätte ich jetzt auch Beispiele basteln können, in denen der Unterschied zwischen winkel- und flächentreu kaum erkennbar ist…
Geht es dem Prof dabei tatsächlich um beliebige Ausschnitte?
Da ich Dir leider nicht wirklich weiterhelfen kann: Ist Dein Englisch gut genug, Deine Frage in einem englischsprachigen Forum zu wiederholen?
Wenn ja, empfehle ich:
https://www.mapthematics.com/f…
Dort ist zwar auch nicht soo viel los, dafür ist der Forumsbetreiber selbst auf jeden Fall ein echter Profi in diesem Bereich.
Tobias Jung
Das Schöne an diesem Atlas ist, dass bei (fast) allen Karten genau dabei steht, welche Projektion verwendet wurde. Wenn man die genau studiert, kann man das Erkennen von Entwürfen bestimmt ganz gut trainieren. Dummerweise braucht das sicher seine Zeit, und ich weiß noch sehr gut aus eigener Erfahrung, dass Zeit etwas ist, was im Studium oft fehlt. Wie auch immer, FALLS das für Dich interessant wäre, diesen Atlas bekommt man z.B. hier:
http://www.booklooker.de/B%C3%…
Tut mir leid, dass ich da keine größere Hilfe sein kann. :-/ Trotzdem viel Erfolg!
SF
Habe mir schon gedacht, dass das nicht so einfach wird. Ich kann leider nicht genau sagen, was er unter "Kartenausschnitt" versteht. Ich habe das so wie oben geschrieben verstanden und einige andere aus meinem Studiengang wohl auch.
Falls eine Projektion mit der gesamten Erde abgebildet wird, wäre das wohl etwas einfacher zu erkennen schätze ich oder?
Also polständig, äquatorständig und zwischenständig, sowie Azimutal,- Kegel- oder Zylinderentwurf sind meistens gut zu unterscheiden finde ich (polständig eher für die Polgebiete geeignet, äquatorständig eher für Projektionen der Äquatorgegend geeignet und zwischenständig z.B. für die gemäßigten Breiten. Oder denke ich mir das zu einfach?)
Schwierig ist dann weiterhin die Verzerrungseigenschaften und das Projektionszentrum zu bestimmen, auch bei Karten wo die gesamte Erde abgebildet ist. Wahrscheinlich ist das eine Lern- und Übungssache.
In deinen 3 Beispielen finde ich es unmöglich, die Verzerrungen einfach zu erkennen muss ich zu geben...
Werde auf jeden Fall mal weiter recherchieren und in dem empfohlenen Forum lesen. Vielen Dank für den Tipp auch mit dem Atlas, vielleicht gibt es da auch eine Ausgabe in unserer Bibliothek von. Und ja das mit der Zeit ist tatsächlich ein Problem ;)
Tobias Jung
> wäre das wohl etwas einfacher zu erkennen schätze ich oder?
Ja, auf jeden Fall.
Tendenziell gilt z.B. bei den Azimutalprojektionen: Eine flächentreue Projektion wird zum Rand hin immer weiter zusammengedrückt, eine winkeltreue zum Rand hin immer weiter auseinander gezogen – und die mittabstandstreue liegt irgendwo dazwischen. Das lässt sich hier auf der Seite ja auch ganz gut sehen.
Flächentreue vs. Mittabstandstreue Azimutalprojektion:
http://kartenprojektionen.de/c…
Mittabstandstreue Azimutalprojektion vs. Stereographische (winkeltreu):
http://kartenprojektionen.de/c…
> polständig eher für die Polgebiete geeignet, äquatorständig eher für Projektionen
> der Äquatorgegend geeignet und zwischenständig z.B. für die gemäßigten Breiten.
> Oder denke ich mir das zu einfach?
Prinzipiell ist das richtig, aber oft muss man schon auch rumprobieren, um den optimalen Projektionspol zu finden (naja, vielleicht schütteln Profis das auch einfach aus dem Ärmel, ich weiß es nicht).
Hinweis:
Dieser Kommentar wurde nachträglich editiert, weil mir viel später aufgefallen ist, dass ich großen Unsinn geschrieben hatte… :-/
Tobias Jung
> Schwierig ist dann weiterhin die Verzerrungseigenschaften
> und das Projektionszentrum zu bestimmen
Das ist wahr. Ich habe das vorhin mal bei ein paar Karten des Atlasses versucht… und bin grandios gescheitert. :-/
Ich fände es aber interessant, so etwas zu lernen – vielleicht ein Projekt, was ich mir für 2016 vornehmen sollte? Im Erkennen von Weltkarten-Projektionen bin ich mittlerweile ganz gut (sicherlich auch noch nicht perfekt); aber solche Ausschnitte korrekt bestimmen zu können, das würde mir gefallen.
> In deinen 3 Beispielen finde ich es unmöglich, die Verzerrungen einfach
> zu erkennen muss ich zu geben...
Das war ja auch der Sinn der drei Beispiele: Zu zeigen, dass man Konfigurationen wählen kann, bei denen eine eindeutige Bestimmung nahezu unmöglich ist. Ich VERMUTE, dass in solchen Fällen auch echte Experten ihre Schwierigkeiten hätten…
Gruß,
Tobias
Martin
Das war ja fast so was wie ein Neujahrsvorsatz, wenn ich mir die posting-Zeit anschaue!
Und ist tatsächlich was draus geworden?
PS.: Danke für deine Seite - ich schau mir gerade die englische Version an und finde alles sehr hilfreich : )
Tobias Jung
leider ist nichts draus geworden – wie das mit vielen Neujahrsvorsätzen so ist. ;-)
Aber vielleicht schaffe ich das doch noch irgendwann mal…
Freut mich, dass Dir die Seite gefällt. Und wenn Du in der englischen Version irgendwelche Übersetzungsfehler entdeckst, sag ruhig Bescheid!
Gruß,
Tobias
Schneider, Friedrich
teile mir bitte mit, woher ich ein nacktes Netz (nur die Netzlinien, ohne Kontinente) für eine Darstellung in Mercator-Projektion (360 Längengrade, ca. 50 bis 60 Breitengrade) bekommen kann.
Vielen Dank und viele Grüße.
Friedrich
Tobias Jung
Selbermachen: G.Projector runterladen https://www.giss.nasa.gov/tool… (läuft auf Windows, Mac, Linux; benötigt eine Java Runtime Umgebung). Beim Start des Programms KEINE Grafik laden. Dann Mercator auswählen, dann gewünschte Werte eingeben für "Max. Latitude", Schrittweite des Netzes, Farben und Strichstärken.
Fertige Karte sichern. Empfehlenswerterweise als PDF, denn dieses kannst Du in Programmen wie Adobe Illustrator, Affinity Designer usw. öffnen und ggf. die Strichstärken und -farben noch einmal anpassen oder die Größe verlustlos ändern. Alternativ kannst Du natürlich auch als PNG oder TIFF sichern, aber das kannst Du dann nicht mehr so einfach anpassen.
Ich kann so eine Grafik auch anfertigen, ABER dann brauche ich VORHER ein paar Angaben: Wieviele Breitengrade genau, und eben die o.g. Werte (Strichfarbe & -stärke, Größe der Grafik), welches Dateiformat… denn ich will das nur einmal machen, und nicht zehnmal, bis das Ergebnis wie gewünscht ausfällt. ;-)