Gruppen der Projektionsarten, Kurzübersicht
Da man in der Auswahl mit Vorschau-Bildern und der Einzelansicht nach Projektions-Typ filtern kann, möchte ich nun auch eine kurze Übersicht der angebotenen Typen liefern.
Ich werde mich hauptsächlich auf die optischen Unterschiede beschränken; ich erkläre hingegen nicht, wie sie mathematisch konstruiert werden oder wie sie zu ihren Bezeichnungen gekommen sind.
Zylinderprojektionen
Beispiel: Die rechteckige Plattkarte
Zylinderprojektionen sind rechteckig, Meridiane und Breitenkreise sind gerade Linien, die
rechtwinklig zueinander stehen.
Zumindest in der üblichen äquatorständigen Ansicht – wenn der Äquator also
vertikal mittig liegt und sich gerade von links nach rechts zieht.
In anderen Ansichten krümmen sich die Linien, ein Beispiel ist die
Cassini-Projektion.
Sind alle rechteckigen Projektionen Zylinderentwürfe?
Nein, auch wenn ich an dieser Stelle lange Zeit etwas anderes behauptet habe.
Ihr dürft mir eben auch nicht alles glauben. ;-)
Adams konforme Erde in einem Quadrat I
z.B. ist rechteckig und keine Zylinderprojektion.
Natürlich darf man auch nicht vergessen: Wenn nicht die gesamte Erdoberfläche gezeigt wird, ist es
immer möglich, dass nur ein rechteckiger Ausschnitt aus einer Projektion, die ganz und gar nicht rechteckig ist,
gewählt wurde.
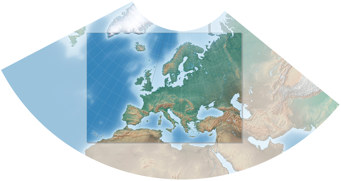
Ein rechteckiger Ausschnitt aus Lamberts winkeltreuer konischer Projektion.
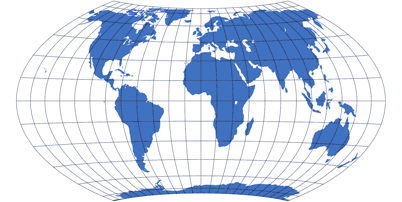
Pseudozylinder oder unecht-zylindrische Projektionen
Beispiel: Wagner VI
Pseudozylinder haben gerade Breitenkreise und einen geraden Mittelmeridian, alle anderen Meridiane sind gebogen – oder, in Ausnahmefällen (z.B. Eckert II), geknickt.
Die Pole werden meistens als Linie darstellt (s. schematische Darstellung von Wagner VI), aber auch punktförmig, wobei sie entweder spitz zu laufen (z.B. Sinusoidal) oder einfach den oberen und unteren Scheitelpunkt einer Ellipse (z.B. Mollweide) darstellen.
Die Meridiane sind auf jedem Breitenkreis gleichabständig eingeteilt. Daher sind einige Projektionen, die auf den ersten Blick wie Pseudozylinder aussehen mögen, unter den Sonstigen zu finden – bei ihnen fehlt diese Eigenschaft.
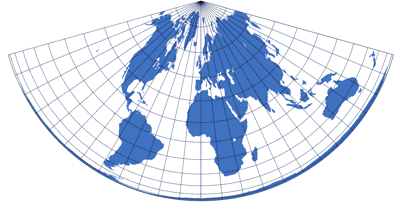
Konische oder Kegelprojektionen
Beispiel: Lamberts flächentreue Kegelprojektion
Komische Konische Projektionen sind kegelförmig…
oder eher, in der Form eines Kegels, den man entrollt hat.
Sie werden üblicherweise nicht für Weltkarten benutzt, sondern eher ausschnittsweise für die Darstellung einzelner Ländern
oder Kontinente. Eine Ausnahme bildet z.B. Schjerning I, die für die
Darstellung der gesamten Welt konzipiert wurde.
Darüber hinaus kann man verschiedene konische Projektionen so konfigurieren, dass sich ein halbwegs vernünftiges
Abbild der gesamten Erdoberfläche ergibt. In den meisten Fällen ist es aber besser, zu einer Projektionen
einer anderen Gruppe zu greifen.
Ich habe hier auf der Site ein paar konische Projektionen mitaufgeführt; aber hauptsächlich der Vollständigkeit halber
und weil ich denke, dass sie interessant aussehen. Meistens dürfte es nicht sinnvoll sein, sie mit anderen Projektionen zu vergleichen.
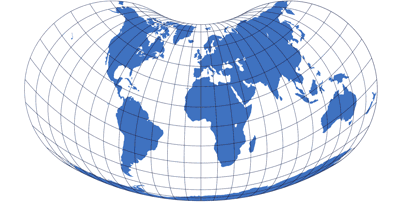
Lentikuläre Projektionen
Beispiel: Wagner VII
Lentikuläre Netzentwürfe ähneln den Pseudozylindern. Während bei diesen aber nur die Meridiane gekrümmt werden, weisen die lentikulären auch gekrümmte Breitenkreise auf.
Der Begriff lentikulär (linsenförmig – im Sinne einer optischen Linse; nicht der Linse, die wir in die Suppe werfen)
wurde vorgeschlagen von Daniel »daan« Strebe in seinem (englischen) Artikel
Map Projection Essentials (dort natürlich als lenticular;
übrigens ein äußerst empfehlenswerter Artikel).
Soweit mir bekannt ist, bin ich
der erste, der diesen Begriff in die deutsche Sprache übernimmt. Auch im englischen Sprachraum scheint der Begriff
noch keine weite Verbreitung gefunden zu haben.
Warum also habe ich mich trotzdem entschieden, ihn zu übernehmen?
Der Grund ist der folgende: Es gibt keinen allgemein anerkannten Sammelbegriff für die Entwürfe,
die hier (und bei Strebe) als lentikulär zusammengefasst werden.
Manche Autoren teilen sie, der mathematischen Herkunft folgend, in mehrere Gruppen ein,
welche dann pseudoazimutal, modifiziert-azimutal, polykonisch usw. benannt werden.
Andere Autoren fassen sie, wie ich, ebenfalls in einer Gruppe zusammen, aber nennen die dann alle »polykonisch«.
Das ist insofern problematisch, als dass diese Gruppe dann Projektionen enthält, die tatsächlich
polykonisch sind – in dem Sinne, dass sie von den o.g. konischen abgeleitet wurden, wie z.B. der
American Polyconic
– und andere, für die das nicht gilt.
Und wieder andere packen sie alle in die Klasse der Sonstigen – die dann plötzlich eine große Menge an Projektionen enthält,
was in meinen Augen ungünstig ist: Unter Sonstiges sollte man immer nur eine kleine Anzahl abheften; nämlich das,
was man wirklich nicht anders bezeichnen kann.
Außerdem gefällt mir der Begriff lentikulär sehr gut!
Er wird auch für Galaxien, die eine bestimmte Form haben benutzt – und was für Galaxien gut ist,
kann für Kartennetzentwürfe nicht schlecht sein. ;-)
Also vielen Dank, daan!
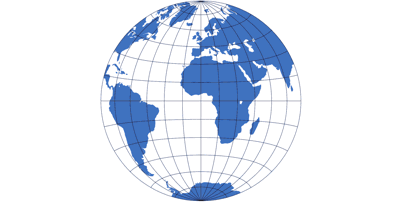
Azimutale Projektionen
Beispiel: Lambertsche Azimutalprojektion
Azimutale Projektionen sind rund.
Man kann etwa vorstellen, dass eine Lichtquelle durch die Erdkugel scheint und eine Projektion auf eine platte Leinwand wirft:
Da eine Kugel immer ein kreisförmiges Abbild erzeugen wird, sind auch die azimutalen rund.
Gut, das ist eine etwas plumpe Erklärung, aber prinzipiell stimmt sie schon.
Sie erklärt auch, warum azimutale Projektionen entweder nur eine Hemisphäre der Erde zeigen – oder, wenn sie auf die gesamte
Erde ausgedehnt wurde, am Rand erhebliche Verzerrungen aufweist.
Es gibt aber auch Projektionen, die rund sind, ohne zu den azimutalen zu gehören.
Früher wurden auch komplette Azimutalprojektionen oft in Atlanten verwendet, meist um die in Hemisphären aufgeteilte Erde zu zeigen (wie ich das am Beispiel der flächentreuen Azimutalprojektion zeigt habe). Heutzutage werden sie, wie die konischen, oft nur ausschnittsweise verwendet, so dass ihre eigentlich runde Form dann nicht mehr erkennbar ist.
Außerdem möchte ich noch darauf hinweisen, dass nicht alle runden Projektionen azimutale sind – manche gehören auch, wie Van der Grinten I, in die Gruppe der Sonstigen.
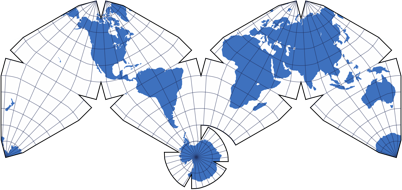
Polyedrische Projektionen
Beispiel: Cahill-Keyes-Projektion
Die Gruppe der polyedrischen Projektionen habe ich erst Anfang 2019 zu meiner Website hinzugefügt. Hauptsächlich deshalb, weil ich zuvor nur wenige Grafiken dieses Typs erzeugen konnte. Bei diesem Typ wird die Erde auf ein, nun ja, ein Polyeder (Vieleck) projiziert (dazu zählt auch ein Dreieck), was zu äußerst ungewöhnlichen Außenformen der Karte führt.
Manchmal lassen sich diese Karten auseinanderschneiden und anders wieder zusammensetzen, was dann – wie bei Kunimune’s IMAGO – zu einer rechteckigen Karte führt. Nichtsdestoweniger zählen natürlich auch diese Ergebnissen zu den polyedrischen.
Die Verwendung einer polyedrischen Projektion kann zu vergleichsweise geringfügigen Verzerrungen der Formen und Flächen führen, oder wenigstens zu einer geringen Varianz an Verzerrungswerten.
Sonstige
Beispiel: Hills euzyklischer Entwurf
Und schließlich haben wir noch die Gruppe der Sonstigen, die ganz einfach all jene Projektionen enthält, die nirgendwo anders reinpassen – nicht einmal in die Klasse der Lentikulären, die ja selbst schon so etwas wie ein Sammelbecken ist.
Und die unterbrochenen Projektionen?
Beispiel: Goode Homolosine
Die unterbrochenen Projektionen gehören eigentlich gar nicht in eine eigene Gruppe! Sie gehören jeweils in eine der anderen Gruppen (meist zu den Pseudozylindern).
Nichtsdestoweniger erschien es mir, da es hier um den Vergleich von Projektionen geht, lange Zeit sinnvoll
sie in einer eigenen Gruppe zusammenzufassen, so dass man sie in der Auswahl mit Vorschau-Bildern
per Filter auswählen konnte.
Mittlerweile aber erscheint es mir sinnvoller, sie unter ihrer eigentlichen Gruppe zu listen.
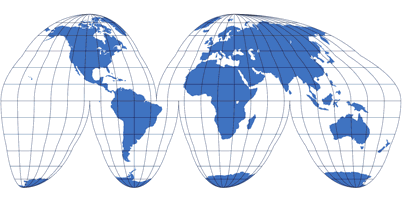
Nachdem das nun geklärt ist, möchte ich noch erwähnen, worin der Vorteil der unterbrochenen Projektionen zu finden ist:
Wenn man bedenkt, dass es unmöglich ist, die runde Erdoberfläche verzerrungsfrei auf eine platte Karte zu projizieren, ist es nachvollziehbar,
dass gewisse Unterbrechungen dabei helfen, Verzerrungen von Größen und Formen zu minimieren.
Schließlich kann man auch die abgepellte Schale einer Orange (um ein populäres Beispiel zu zitieren) nicht flach auf einen Tisch legen, ohne sie an einigen Stellen einzureißen. Man könnte also sagen, dass die Herangehensweise, eine Kartenprojektion mit Unterbrechungen anzufertigen, von der Alltagswelt inspiriert ist…
Zurück zu Grundwissen • Nach oben
Kommentare
Ein Kommentar
Es gibt weitere Kommentare in der englischen Version.
Tobias Jung
Unter Strich hast Du aber schon Recht, mit den polyedrischen, aufgeschnittenen Entwürfen kommt man schon sehr nahe an eine Projektion, die Größen- und Formverzerrungen soweit reduziert, dass sie mit bloßem Auge kaum mehr wahrnehmbar sind. In diesem Blogpost habe ich winkeltreue Projektionen gezeigt, welche äußerst geringe Vergrößerungswerte besitzen:
https://blog.kartenprojektione…
Es wäre m.E. sehr interessant, einen umgekehrten Fall zu sehen, also eine flächentreue polyedrische Projektion, um zu prüfen, wie es sich dort mit den Winkelverzerrungen verhält; oder weitere Beispiele wie die Dymaxionkarte, also vermittelnde Polyeder. Leider sind mir derartige Beispiele nicht bekannt.