Wagners Netzentwürfe (Teil 1)
Die neun Entwürfe von Karlheinz Wagner sind alles andere als neu – sie wurden zwischen 1932 und 1949 entwickelt – und dürften allen, die sich für Kartennetzentwürfe interessieren, ein Begriff sein. Sie wurden in der Vergangenheit auch schon in diversen Atlanten verwende; aber in den letzten Jahren scheinen sie mir allmählich in Vergessenheit zu geraten. Und das haben sie nun wirklich nicht verdient.
Da ich Wagner Arbeit wirklich schätze, und da man die neun Entwürfe selten mal in einer zusammenhängenden Darstellung sieht (abgesehen von Dr. Böhms sehr empfehlenswerten Artikel Wagners Weltkartennetze, möchte ich sie an dieser Stelle präsentieren.
Und da man über neun Projektionen ziemlich viel reden kann, habe ich mich entschlossen, den Artikel in mehreren Teilen zu veröffentlichen.
Teil 2 zeigt eine Anwendungsbeispiele,
Teil 3 behandelt das Umbeziffern etwas näher,
Teil 4 zeigt Wagners durch Umbeziffern generierte flächentreue Varianten des Wagner VII,
Teil 5 wird (hoffentlich) bald die Varianten von Canters und Böhm zeigen…
Einleitung
Wagner hat keine Projektionen komplett neu entwickelt – statt dessen hat er auf bestehende Entwürfe ein Verfahren namens Umbeziffern von Kartennetzen angewendet, welches ihm erlaubte, Entwürfen mit einem polförmigen Punkt eine Pollinie zu verpassen, und das Resultat weiter zu modifizieren.
Klingt das zu theoretisch?
Okay, sehen wir uns das genauer an:
- Wagner I, II und III sind durch Umbeziffern von der Sinusoidal-Projektion abgeleitet;
- Wagner IV, V und VI stammen von der Mollweide-Projektion ab;
- Wagner VII, VIII und IX sind Nachkommen (modifizierter) äquatorständiger Azimutalentwürfe.
Soweit also die Vorfahren der Wagner-Projektionen – und wie hat Wagner diese »weiter modifiziert«?
- Wagner I, IV und VII sind, wie ihre Vorgänger, flächentreu (wurden nach dem Umbeziffern also nicht weiter modifiziert);
- Wagner II, V und VIII führen eine (eher geringe) Flächenverzerrung ein, um die Wiedergabe der Formen zu verbessern (oder, wissenschaftlicher gesprochen, um die Winkelverzerrung zu reduzieren);
- und Wagner III, VI sowie IX geben die Flächentreue ganz auf und setzen auf Abweitungstreue – was in diesem Fall heißt, dass die Parallelkreise gleichabständig dargestellt werden.
Hier noch einmal die gleiche Aufstellung innerhalb einer übersichtlichen Tabelle:
| Stammvater | Flächentreu | Vermittelnd | Abweitungstreu |
|---|---|---|---|
| Sinusoidal-Projektion |
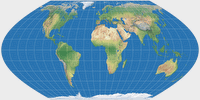
Wagner I |
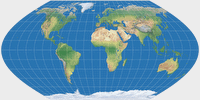
Wagner II |
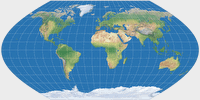
Wagner III |
| Mollweide |
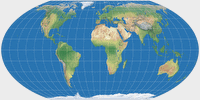
Wagner IV |
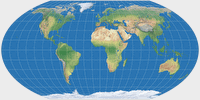
Wagner V |

Wagner VI |
| Äquatorständige Azimutalentwürfe |
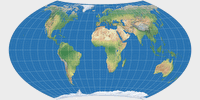
Wagner VII |
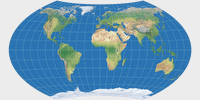
Wagner VIII |
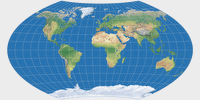
Wagner IX |
Bevor wir die Wagner-Entwürfe einzeln betrachten und etwas näher analysieren, möchte ich noch zwei Hinweise loswerden:
– Die Ordnungszahlen entsprechen nicht der Reihenfolge, in denen Wagner seine Entwürfe entwickelt hat, sondern der Reihenfolge,
in denen er sie in seinem Buch Kartographische Netzentwürfe [1]
vorstellt.
Die Nummerierung wurde von J.P. Snyder [2]
vorgenommen, Wagner selbst hat diese Bezeichnung nicht genutzt.
– Bei den Entwürfen II, V und VIII sprach Wagner von einer vorgeschriebenen Flächenverzerrung, was sich auf die (von Wagner selbst gesetzte) Einschränkung, dass die Flächenvergrößerung zwischen 60° Nord und Süd nicht mehr als 20% betragen sollte. Innerhalb dieses Bereich deckt man den größten Teil der bewohnten Gebiete der Erde ohne übertriebene Flächenverzerrungen ab.
Wagner I, II und III – Die Sinuisoidal-Abkömmlinge
Wagner I (flächentreu)
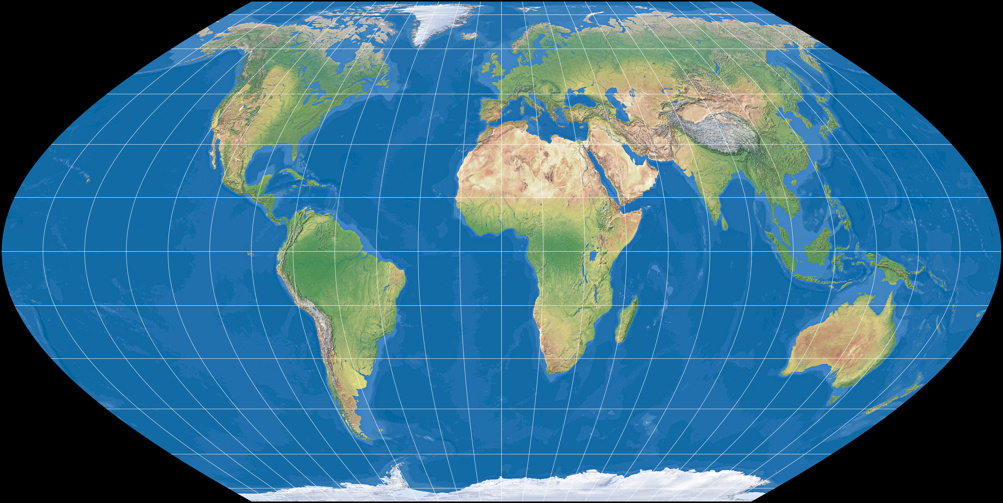
Wagner II (moderate Flächenverzerrung)
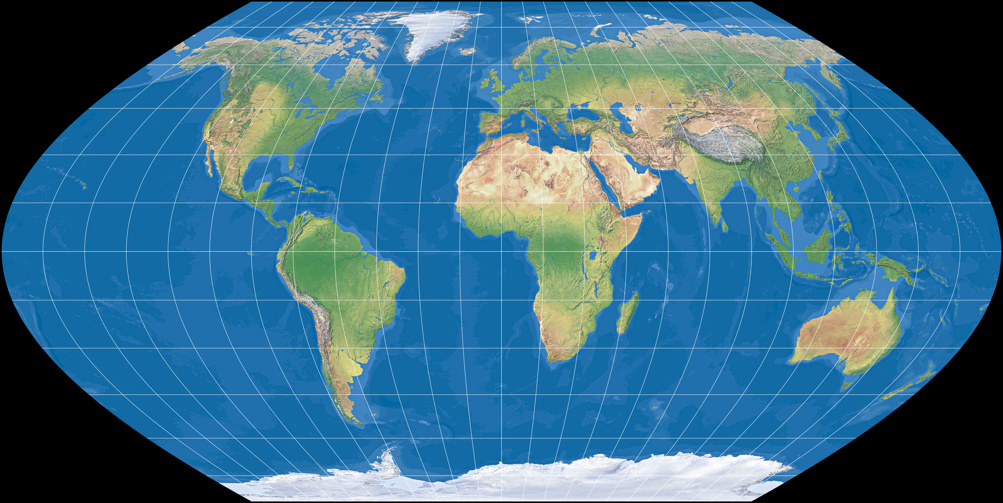
Wagner III (gleichabständige Parallelkreise)

Es ist sehr schön zu sehen, wie sich die Entwürfe II und II einerseits schrittweise von der Flächentreue des ersten Entwurfs entfernen,
andererseits die Formtreue erhöhen.
Experten wird allerdings auffallen, dass Wagner I fast identisch ist zum fast 30 Jahre früher entstandenen Eckert VI,
während Wagner III eine auffallende Ähnlichkeit zu Eckert V zeigt:
Eckert VI vs. Wagner I –
Eckert V vs. Wagner III
Wagner weist in seinem Buch Karthographische Netzentwürfe ausdrücklich auf diese Ähnlichkeit hin.
Warum also hat er diese Projektionen überhaupt entworfen?
Einfach gesagt: Die Formeln von Wagner sind einfacher zu verarbeiten als jene von Eckert.
Man muss bedenken, dass zu jener Zeit keine Computer oder andere elektronsiche Rechenhilfen zur Verfügung standen,
folglich war es tatsächlich von Bedeutung, eine mathematische Formel zu vereinfachen.
Der Wagner III weist außer seinen gleichabständigen Parallelkreisen noch eine weitere metrische Eigenschaft auf: Er ist längentreu im Mittelmeridian und Äquator. Wagner schlug darüber hinaus vor, dass man einen anderen Parallelkreis längentreu abbilden könne (ohne die Längentreue den Mittelmeridians zu ändern), um »eine bessere Verteilung der Verzerrungen« zu erreichen. Eine derartige Darstellung mit 40° Nord/Süd ist hier auf der Website enthalten.
Zum optischen Eindruck dieser Entwürfe: Sehen sie nicht etwas… merkwürdig aus?
Heutzutage sind Projektionen mit sinusförmigen Meridianen sehr selten, man bekommt – bei nicht-zylindrischen Entwürfen
– fast ausschließlich
ellipsenförmige Meridianbögen zu sehen (zu denen wir noch kommen werden); aus dem einfach Grund, dass die elliptischen
Varianten zumeist mit einer geringen Formverzerrung auskommen.
Während Wagners (und auch Eckerts) Sinuslininen-Entwürfe in gewissen Bereichen tatsächlich Vorteile gegenüber den Ellipsen-Entwürfen haben (nämlich in direkter Nähe zu den Polen), so würde ich unterm Strich doch stets den letztgenannten den Vorzug geben – es sei denn, man entscheidet sich bewusst für eine eher ungewohnte Darstellungsweise: Auch das kann ja, in der Funktion als »eye-catcher«, schon mal eine gute Idee sein. Darüber hinaus kann ich mir eine Situation vorstellen, in der die Sinus-Variante tatsächlich Vorzüge haben kann – darauf komme ich in Teil 2 des Artikels zurück.
Aber sehen wir uns nun Wagners Entwürfe mit Ellipsenbögen an…
Wagner IV, V und VI – Die Mollweide-Abkömmlinge
Wagner IV (flächentreu)
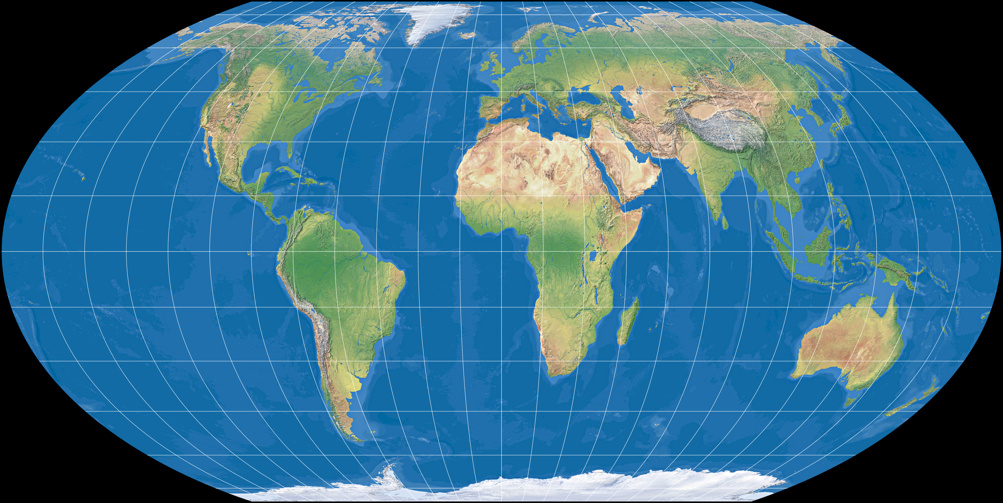
Wagner V (moderate Flächenverzerrung)
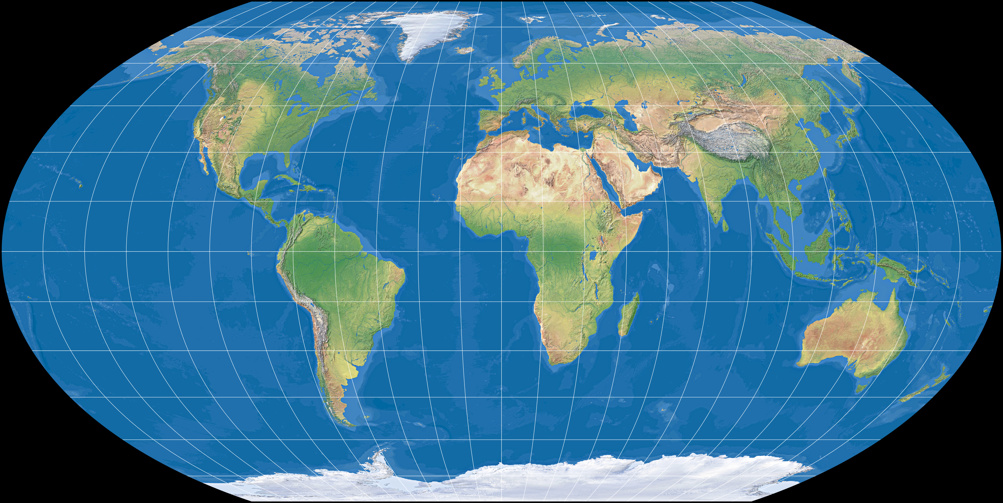
Wagner VI (gleichabständige Parallelkreise)
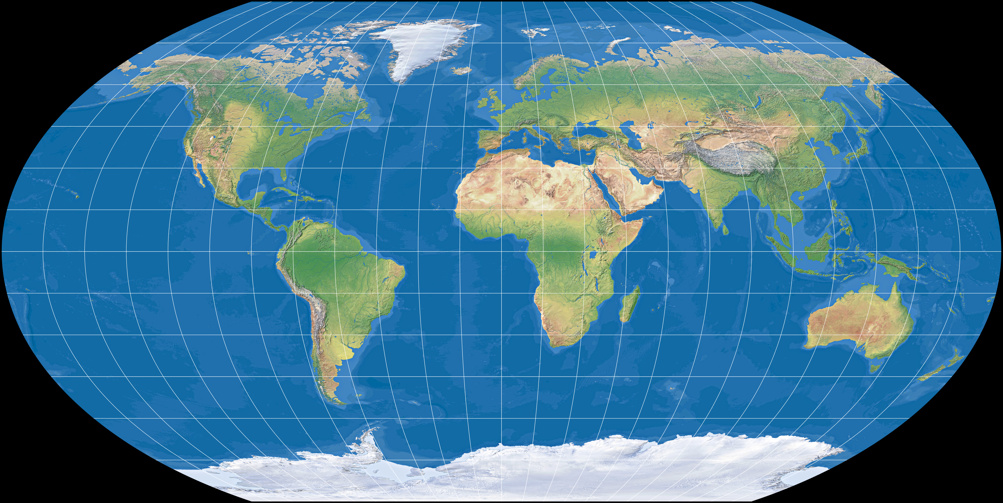
Wir sehen die gleiche Transformation – von flächen- zu abweitungstreu – wie bei der ersten Reihe.
Und abermals gibt es eine gewisse Ähnlichkeit zu Eckerts Entwürfen, jedoch fällt sie nicht annähernd
so stark aus wie zuvor:
Wagner IV vs. Eckert IV –
Wagner VI vs. Eckert III
Deutlich erkennbar ist die stärkere Krümmung der Ellipsenbögen bei Wagners Entwürfen –
und natürlich, die spitzen Ecken am Ende der Pollinien im Gegensatz zu den abgerundeten Ecken bei Eckert.
Und obwohl die Eckert-Entwürfe geringfügig bessere Verzerrungswerte aufweisen
[3]
[4],
ziehe ich die Wagner-Projektionen vor:
Mir gefallen einfach die stärkeren Krümmungen, die spitzen Ecken – und die weniger ausgeprägte Streckung
der polnahen Gebiete.
Zugegebenermaßen wird die Form Australiens bei Eckert besser dargestellt…
Zu den drei Entwürfen diese Reihe im Einzelnen:
Die Nützlichkeit flächentreuer Projektion muss, denke ich, nicht weiter diskutiert werden,
und sowohl der Wagner IV als auch der Eckert IV sind m.E. ganz hervorragende Vertreter dieser Gattung.
Ob man hier nun der Wagner- oder der Eckert-Variante den Vorzug gibt, ist wohl eine reine Geschmacksfrage.
(Übrigens: Ich brauchte sie eigentlich nicht, aber aus reinem Spaß an der Freude habe ich Wagner-IV-Annäherung
gebastelt, die man im Flex Projector verwenden kann. Mehr darüber im
Kapitel Approximationen.)
Wagner V ist eine sehr gute vermittelnde Projektion, wenn man einen Pseudozylinder braucht, der sich nicht allzu weit von der Flächentreue entfernt. Ein entsprechendes Gegenstück fehlt bei Eckert, allerdings bietet z.B. die Software Geocart einen Mittelweg zwischen Eckert III und IV an – und mit dem »Simple Mixer« von Flex Projector kann man sich leicht eine entsprechende eigene Projektion herstellen, so dass man dann doch wieder ein Eckert-Äquivalent zum Wagner V hat.
Mix von Eckert III und Eckert IV (links), zum Vergleich noch einmal der Wagner V (rechts)
Wie bereits gesagt, hat der Wagner VI gleichabständige Parallelkreise – welchen Sinn und Zweck hat diese Eigenschaft eigentlich?
Nun, es ist ziemlich offensichtlich, dass dies zu vergleichsweise geringen Formverzerrungen führt, gerade in den hohen Breiten
– aber dafür zahlt man einen Preis. Wagner selbst hat dies so ausgedrückt:
Die Zunahme der Flächenvergrößerung ist doch schon recht erheblich.
Augenscheinlich bevorzugte Wagner die Entwürfe »mit vorgeschriebener Flächenverzerrung« – wobei er aber wiederholt darauf hinweist, dass man für diese Flächenverzerrung auch andere Parameter wählen kann, als er vorgestellt hat. Abermals verweise ich auf kommenden Teil 2 dieses Artikels, in dem ich darauf näher eingehen und auch Anwendungsmöglichkeiten für abweitungstreue Projektionen zeige werde.
Nun möchte ich zu der Reihe kommen, die mir am interessantesten erscheint.
Wagner VII, VIII und IX – Die azimutalen Abkömmlinge
Wagner VII (flächentreu)
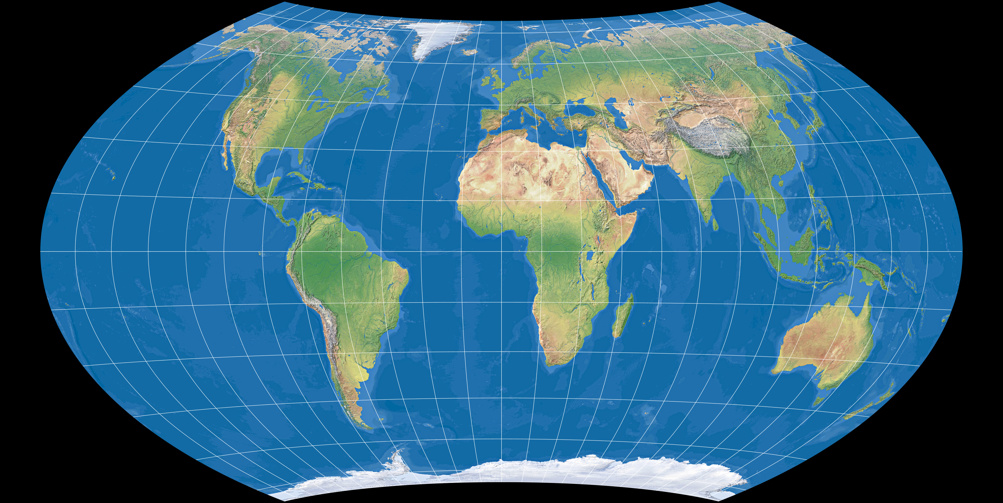
Wagner VIII (moderate Flächenverzerrung)
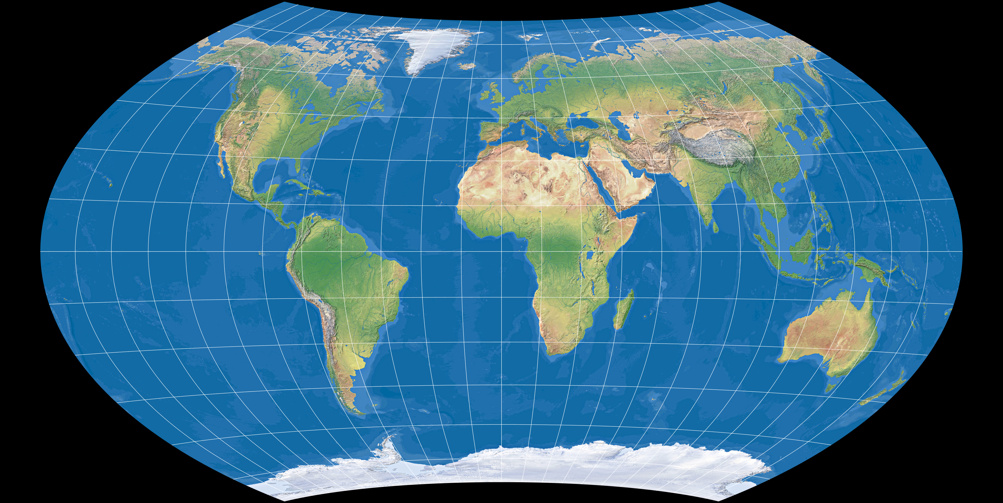
Wagner IX (gleichabständige Parallelkreise)
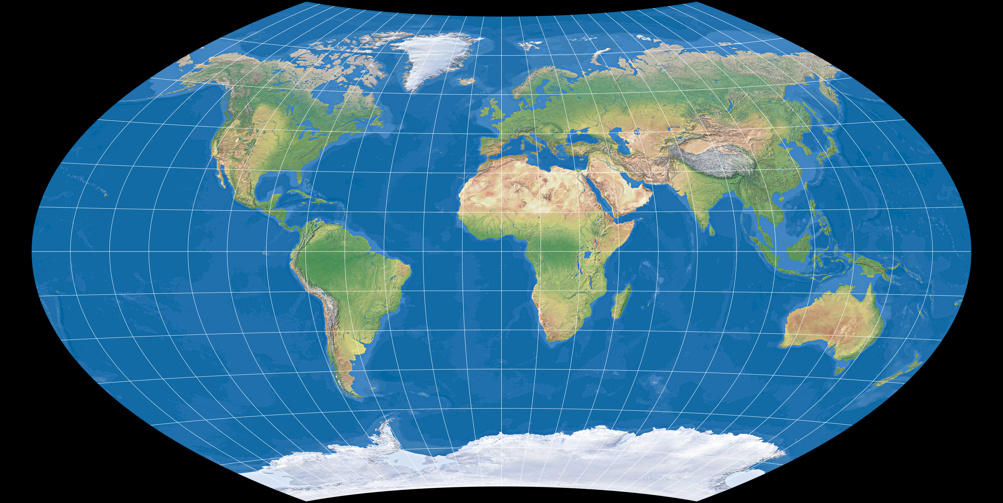
Wagner VII ist eine Weiterentwicklung des Hammer-Entwurfs, die mit einer Pollinie versehen wurde – und da der Hammer seinerseits eine Weiterentwicklung des querachsigen flächentreuen Azimutalentwurfes darstellt, ist auch Wagners Projektion flächentreu. Die gebogenen Breitenkreise reduzieren die Formverzerrungen am Rande der Projektion und dadurch erhalten wir eine sehr schöne, ausgewogene Darstellung der Erde – einer meiner beiden absolute Favoriten unter den flächentreuen Projektionen! (Der andere Favorit ist übrigens der Strebe 1995.)
Wagner VIII ist das Gegenstück zum Wagner II bzw. Wagner V: Abermals entwickelt Wagner eine Projektion
mit vorgeschriebener Flächenvergrößerung aus dem flächentreuen Modell.
Mir wurde zwar nahegelegt:
Die Verbesserungen für Afrika und Südamerika sind geringfügig (…) Ich sage: Wenn Du Dich von der Flächentreue verabschiedest,
sei mutig! [4]
… dennoch gefällt mir der Wagner VIII sehr gut! In meinen Augen ist die Verbesserungen auch gar nicht soo geringfügig.
Die vertikale Streckung von Afrika (und übrigens auch Australien) wird angenehm reduziert:
Wagner VII vs. Wagner VIII
Obwohl ich auch zugeben muss: Diese Unterschiede stechen vor allem beim direkten Vergleich ins Auge. Auch ich habe beim Anblick einer Weltkarte in einem Atlas schon eine Weile überlegen müssen, ob ich mir gerade den Wagner VII oder den Wagner VIII ansehe…
Nichtsdestoweniger halte ich an meiner Meinung fest, dass der Wagner VIII eine höchst empfehlenswerte Projektion darstellt, gerade für den allgemeinen Gebrauch, also z.B. für Wandkarten oder die Weltkarte in Schulatlanten. Es sei denn, man legt Wert auf absolute Flächentreue – dann ist der Wagner VII eine hervorragende Alternative, welche die korrekten Größenverhältnisse ohne allzu verbrecherische Formverzerrungen abbildet.
Und letztendlich kommen wir zum abweitungstreuen Vertreter der Reihe mit gekrümmten Breitenkreisen.
»Abweitungstreue« liegt hier, eben wegen der nicht-konzentrischen Krümmung, natürlich nur entlang des zentralen Meridians vor.
Der Wagner IX zeigt daher eine Flächenvergrößerung, die mehr oder weniger der Verzerrung von Wagner III und VI entspricht.
Aber seltsamerweise empfinde ich sie hier als weniger störend.
Vielleicht liegt das gerade an der Krümmung, welche bedingt, dass z.B. Grönland eine etwas geringere horizontale Streckung aufweist…
Und daher kann ich sagen: Mit Bedacht eingesetzt, kann der der Wagner IX ein guter Kandidat für Weltkarten allgemeinen Gebrauchs sein.
Vielleicht mit einer kleinen Modifikation:
Wagner weist abermals darauf hin, dass ein horizontales Stauchen der gesamten Projektion »eine Verbesserung in der Verteilung
der Verzerrung« zur Folge hat und zeigt ein Beispiel, in dem die horizontalen Werte zu diesem Zweck mit einem Wert von 0,88 multipliziert
wurden. Diesen Wert hat er gewählt, um seine Projektion an die äußere Form des Winkel Tripel anzunähern (die schon damals in Deutschland
äußerst populär gewesen zu sein scheint).
Mir selbst fällt diese Stauchung ein wenig zu hoch aus. Aber schließlich hat Wagner sie ja auch nur als Beispiel genannt.
Es kann also jeder selbst herausfinden, ob man mit einem Faktor wie etwa 0,92 oder so besser bedient ist.
Zwischenfazit
Wagner hat eine nahezu universell einsetzbare Familie an Weltkarten-Projektionen vorgelegt. Mit der Auswahl von sinus- und ellipsenförmigen Meridianen, geraden oder gebogenen Breitenkreisen in jeweils drei verschiedenen metrischen Eigenschaften, schrittweise von der Flächen- zur Abweitungstreue gehend, werden fast alle denkbaren Einsatzmöglichkeiten von Weltkarten abgedeckt (solange man von nicht-unterbrochenen Entwürfen mit Pollinie ausgeht).
Im zweiten Teil des Artikels möchte ich das anhand einiger Beispiele zeigen.
Quellenangaben
-
↑
Wagner, Karlheinz:
Kartographische Netzentwürfe.
Leipzig 1949. -
↑
Snyder, John P.:
Flattening the Earth: Two Thousand Years of Map Projections.
Chicago 1993. -
↑
Capek, Richard 2001:
Which is the Best Projection for the World Map?
icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf - ↑ siehe die Distortion Value Tables in Flex Projector
- ↑ gepostet von daan Strebe während einer Diskussion im Forum von mapthematics.com
Zurück zu Ausgewählte Entwürfe • Wagners Netzentwürfe (Teil 2) • Nach oben
Kommentare
Sei der erste, der einen Kommentar hinterlässt!